I have seen countless sites saying electrons flow from higher potential to lower potential, but then again I have seen many saying that electrons flow from lower potential to higher.
I have always imagined it as a hill which is a high potential and the bottom of the hill as a lower potential.
I'm just confused about which one it is. Higher to lower potential or lower to higher to lower potential.
Electrons flow from low to high potential. This is because they have negative charge, so lower potential means higher potential energy.
Current is a flow of charge. Let's forgetabout the magnetic field and consider just electrostatics.
A particle with charge \$ q \$ in an electric field \$ \vec{E} \$ experiences a force \$ \vec{F} = q\vec{E} \$.
The electric field \$ \vec{E} \$ is the gradient of the electric potential \$ V \$, which is a scalar field. \$ \vec{E} \$ is a vector field.
As you can see from the product \$ \vec{F} = q\vec{E} \$, the sign of the force depends on the sign of the charge and the sign of the field.
So, if a conducting path is available, like a wire, or a conductive fluid like water, negative charges (electrons, negative ions...) will flow towards more positive potential, whereas positive charges (positive ions, etc) will flow towards more negative potential. That's just another way to say "opposite charges attract each other".
If the electrons bump into atoms on the way, they won't pick up speed, instead they will travel at a rather constant speed and shed their kinetic energy along the way, giving it to the atoms they bump into, heating the medium, and you get a resistor. If it happens in vacuum, then the electrons will pick up speed and crash into whatever obstacle they encounter at the end of the trip, which makes a cathode ray tube, or a triode, or an X-ray emitter...
Charges tend to move from high potential energy to low potential energy, as this means that the electrical field is doing work on them. If a charge goes from low potential energy to high potential energy, that means the charge is doing work on the electrical field (arguably, in a circuit, charges going from high to low must be balanced by the reverse, but the latter is done by the EMF and is generally omitted from analysis of current flow).
Potential energy is coulombs times voltage. The unit of "coulomb" was chosen in such a way that an electron is "negative", so a "decrease" in voltage corresponds to an increase in electron potential energy, while an "increase" in voltage corresponds to a decrease in electron potential energy, but those are arbitrary choices, and "negative" charges and "negative" or "lower" voltages aren't really "negative" in an objective sense; while 10 eV is objectively "more" than 5 eV, 10 V is not objectively "more" than 5 V. However, when we talk about voltage on a circuit, we generally are referring to the (absolute value) difference between voltages, so a 10 V circuit does have more voltage difference than a 5 V circuit.
In drift current, electrons flow from a region with a more negative electric potential to a region with a more positive electric potential.
However, drift current is not the only kind of current. There is also diffusion current.
In diffusion current (when it is diffusion current of electrons), electrons flow from a region with a higher concentration or density of free electrons to a region with a lower concentration of free electrons.
It is not always the case that a region of higher electron density is also a region of more negative electric potential. In particular, that is often NOT the case in semiconductors.
Don't confuse potential with potential energy. They are intimately related, as I'll show below, but it will require some explaining. Bear with me! This diagram will help distinguish and relate them:
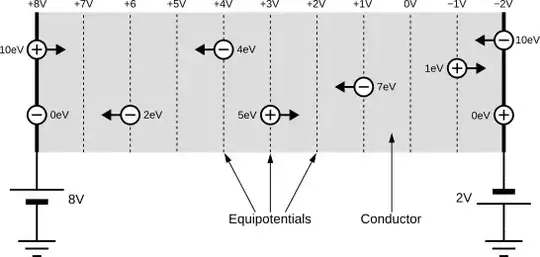
Here we have two conductive plates, separated by some distance, and having some conductive material between them. This could represent a resistor, for example. I have applied fixed potentials of +8V and −2V at each end, using cells, for a total potential difference of 10V from end to end.
Mobile negative charges in the grey material would be electrons. They are represented by circled "−" symbols. They each have charge \$-q\$, where:
$$ q=1.6\times 10^{-19} \rm{C} $$
Even though there would be no mobile positive electric charges in the conductor (unless the material were an electrolyte or something else that actually can contain mobile positive charge carriers), they are represented here by the circled "+" symbols. They have charge \$+q\$.
The entire grey area will have an electric field within in it, due to the 10V potential difference applied to the end plates. If the plates were, say, 10cm apart, that electric field would have strength \$E\$ throughout:
$$ E = \frac{\Delta V}{d} = \frac{(+8V) - (-2V)}{0.1m} = \frac{10V}{0.1m} = 100\frac{V}{m} $$
Notice how it's the potential difference between the two ends that we are interested in. That means we could apply potentials 100V higher at each end, for +108V and +98V, and nothing inside the material changes! Keep that in mind as we go on.
You could use this \$E\$ to calculate the force \$F\$ on each charge. Here, \$Q\$ is the charge (either \$-q\$ or \$+q\$ for my hypothetical charges above):
$$ F=EQ $$
Importantly, the sign of \$F\$ depends on the sign of \$Q\$. This determines the direction of force (and consequently acceleration), and so the positive charges are accelerated in the opposite direction to the electrons. That force (and direction of movement) is represented by the arrows attached to each charge.
Here's the answer to your question, then: electrons travel from low potential to high. That's true for anything that isn't a source of energy. For sources like batteries or solar panels, the story might be different, so for now we are considering only passive elements like resistors, wires and so on.
Understand that even though the "voltage" or "potential" is clearly higher (more positive) on the left here, the potential energy possessed by a charge (relative to same-polarity charges at the other end) depends on the charge's polarity.
Each electron at the right-hand plate has 10eV more potential energy than electrons found at the left hand plate. However, for positive charges it's the other way around; each positive charge at the left plate has 10eV more than positive charges at the right plate.
That's because each charge "falls" in the electric field in the direction of the force it experiences, in the same way that positive mass always falls in a gravity field. You mentioned the ball on a hill, and this can help. A ball at the top of a hill has more gravitational potential energy than it would have at the bottom. When released, it will always roll downhill, and will therefore always lose potential energy. As it rolls, it accelerates, but friction will prevent it from attaining much speed, and in the end, almost all of the potential energy it started with will have been lost to the grass and brush it rolled over, or trees it collided with. It will reach the bottom with no potential energy, and almost no kinetic energy either. This analogy does't have balls with negative mass, though, so it's not perfect.
In the electrical realm, we are dealing with electric fields, not gravitational, and the direction of "falling" is defined by the polarity of the charge. Positive charges "fall" towards lower potentials, as in the gravity analogy, where a positive mass falls to a lower elevation, but electrons, with their negative charge, "fall" towards higher potentials. Perhaps it might make more sense to think of electrons falling "upwards". It's entirely up (or down) to you, how you picture this.
Regardless of polarity, all charges "fall" to a place of lower potential energy, but depending on the charge polarity, that place can have either higher or lower electrical potential, or "voltage".
Just for completeness, since charges always "fall", and always lose potential energy (I say always, but there are of course ways to increase a charge's potential energy, which is another story), that energy must be donated to the environment, to comply with the law of conservation of energy. In a resistor, a charge's potential energy is converted to heat. In a motor, most of the energy would become kinetic (motion) energy. For an LED or lamp, some would become light.
The algebra for current and voltage is charge-agnostic. It works, and is consistent, whether the actual participating charges are positive or negative. However, it's easier to envisage positive charges falling to a lower potential, since we are all familiar with masses falling downwards to a lower position. That's why we use "conventional" current, in which we treat all charges as positive, flowing from high to low potential, even though we are well aware that the actual participating, moving charges are electrons going the other way.
