There is a universal method for determining voltages and currents in a linear circuit - that is, a circuit containing resistors, inductors, capacitors and op-amps.
- Laplace transfrom the input source, the inductors and the capacitors.
- Write a node equation for each node in the circuit.
- Solve the system of equations with respect to the unknown voltages.
- Inverse-Laplace transform the expression for the voltage you are interested in.
Here is an example of @Jonk using that algorithm to find the output voltage of an RL-circuit.
But this algorithm cannot be used on non-linear circuits. Consider a generic flyback converter shown below: -
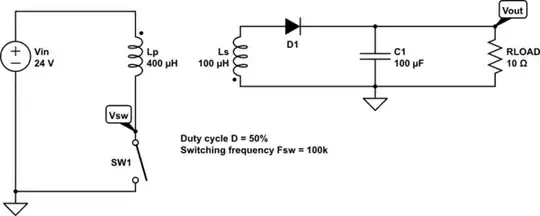
simulate this circuit – Schematic created using CircuitLab
Due to the switch (actually a MOSFET) and the diode the node equations cannot be written up in the usual way. But say I wanted to plot the voltage waveforms for the load voltage (\$V_{out} \$) and the voltage across the switch (\$V_{sw}\$) how would I do that? Can I arrive at an/a piecewise equation for both voltages?