3

I've been doing problems out of my circuit analysis textbook by Ulaby, Fawwazz et al. to study for an upcoming exam.

I am having serious trouble producing a transfer function and with such finding the resonant frequency (which I think will be easier once I figure out how to produce a transfer function a bit more easily). I have tried to do this for a couple circuits, with multiple attempts, to no avail. Any circuits that are beyond the basic parallel RLC's, I get lost in the algebra and can never recreate the results given by the answer key in the textbook/online resources. Unfortunately, we never go in depth during lecture, and my professor has no desire to fully work through a problem with me. I think once I've seen a couple examples fully worked through of circuits beyond the super basic, I should be able to better recreate it.

Here are two of the many circuits that I have utterly failed to produce the transfer function for.

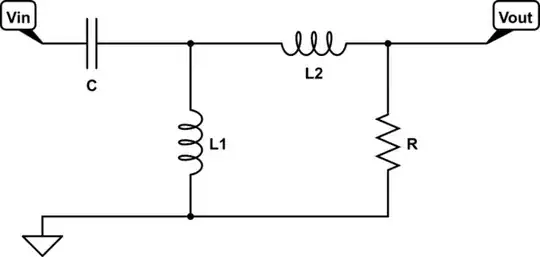
schematic

simulate this circuit – Schematic created using CircuitLab

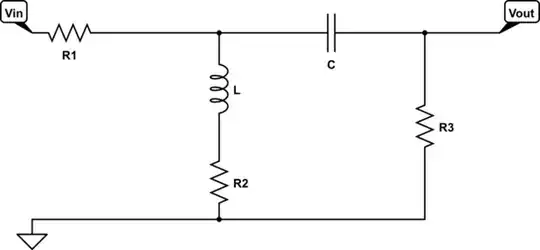
schematic

simulate this circuit

I understand how to produce a simple version of the transfer function for both of these (I think). For both circuits, simple nodal analysis and solving for Vout/Vin gives me: $$ H = \frac{1}{(\frac{L_1 + L_2}{C} + \frac{R}{jwC}+1)(\frac{R+jwL_2}{R})} $$ And for the second one:

$$ H = \frac{1}{ R_1(\frac{\frac{1}{jwC}+R_3}{R_3})(\frac{1}{\frac{1}{jwC}+R_3} + \frac{1}{jwL + R_2} + \frac{1}{R_1})} $$

Beyond this, I've done over a couple hours of algebra trying to simplify and solve for resonant frequency. So, what is the way I can do this with the least pain and have successful results? The latter is the most important because, as I said, I can't get the right answer in the end.

imthegman55
  • 115
  • 9
  • 1
    Do the study materials provide you with the answers? If not, how do you know you don't get the right answer? Do you want standard form for these equations? (There are two such standard forms, in my limited experience, for 2nd order per your second schematic, not the first. So, if so, you may want to say what you are comfortable seeing as a result.) – jonk Apr 09 '22 at 21:55
  • @jonk These questions are in the textbook, and there's an answer key at the back for some questions. Other questions I have looked online for but these ones seldom go into detail. They mostly just say the technique they used and skip to the final answer. I have no specific study materials, just chapters that it covers. The end goal here is resonant frequency for these problems. However, converting to standard form would be great as that is also covered in the exam. As for what "kind" of standard form, I'm not sure what you mean. We discussed simple and quadratic poles/zeros for this class. – imthegman55 Apr 09 '22 at 22:07
  • (1) I guess I'm wanting to know if you have the answers for *these* specific examples, above. Sure, I get the idea of just being generally able to handle them and these are only example cases to point in the direction. But I can't write a textbook on the topic here, while I can of course write specific answers to specific questions (which you have provided.) Assuming I choose to write an answer, I'd like to know if you already possess a "correct" answer for the questions at hand. In short, would you already be able to agree with me if I wrote out an answer? – jonk Apr 09 '22 at 22:13
  • (2) For example, a low-pass 2nd order may take these two standard forms that I know about: $A\frac{\omega_{0}^2}{s^2+2\zeta\omega{0}s+\omega{0}^2}$ or $A\frac{1}{\frac{s}{\omega{0}}^2+2\zeta\frac{s}{\omega{_0}}+1}$. – jonk Apr 09 '22 at 22:13
  • @jonk Yes, I already possess answers to both of these questions. I just can't recreate them. I haven't seen the first standard form example you gave, but I have seen the second one. I'm not sure what the A is. – imthegman55 Apr 09 '22 at 22:17
  • So, what do you know how to use? May I assume you are comfortable setting up KCL and KVL? (I don't see your work process above, just two 'answers'.) If you can do that and solve them, there's not much left to do. (I never use $j\omega$ unless I'm solving for $s\to j\omega$, but instead always use $s$.) – jonk Apr 09 '22 at 22:20
  • @jonk My biggest issue right now is getting from the transfer function I get from KCL/KVL to finding the resonant frequency. I think this issue is mostly algebraic so I was hoping to see some of the steps/manipulations used to get to the final answer. The standard form part you mentioned would be just a bonus but isn't the focus of this post. I'll edit the post to make that more clear – imthegman55 Apr 09 '22 at 22:24
  • I have written a lot of stuff here that may be worth review. Also, something on a little different but broadly related topic here. – jonk Apr 09 '22 at 22:25
  • I guess the problem I have is that I'm not interested in seeing if your second equation (easier to begin with your 2nd order case) is correct. Since you didn't provide the work in achieving it, I'd normally just ignore it and do the KCL myself. What I get is $\omega_{_0}=\frac1{\sqrt{L_1C_1\frac{R_1+R_3}{R_1+R_2}}}$ and that this is a combined high pass and bandpass. – jonk Apr 09 '22 at 22:45
  • I can certainly see that the second answer is wrong already, because it doesn't include a $j\omega L_1$ term. So start by making sure the nodal analysis part is right. – TimWescott Apr 09 '22 at 22:52
  • @TimWescott, Oops, I I wrote a C where there was supposed to be an L. My fault, it was fixed. – imthegman55 Apr 09 '22 at 23:00
  • @imthegman55 It's still not right. How can you add R3 to jwC? To 1/(jwC), sure. But not directly as you show it. If you fix that mistake as well, then I think you may be close. Perhaps you can solve it then? – jonk Apr 09 '22 at 23:04

2 Answers2

6

I'll give you a start, using your newly corrected 2nd order equation.

Below, for simplicity, I replaced \$j\omega\$ with \$s\$:

$$\begin{align*} H &= \frac{1}{ R_1\left(\frac{\frac{1}{s \,C_1}+R_3}{R_3}\right)\left(\frac{1}{\frac{1}{s\,C_1}+R_3} + \frac{1}{s\,L_1 + R_2} + \frac{1}{R_1}\right)} \\\\ &=\frac{R_3}{R_1}\cdot\frac{s \,C_1}{ \left(1+s \,C_1 R_3\right)\left(\frac{s \,C_1}{1+s \,C_1 R_3} + \frac{1}{s\,L_1 + R_2} + \frac{1}{R_1}\right)} \\\\ &=\frac{R_3}{R_1}\cdot\frac{s \,C_1}{ s \,C_1 + \frac{1+s \,C_1 R_3}{s\,L_1 + R_2} + \frac{1+s \,C_1 R_3}{R_1}} \\\\ &=\frac{R_3}{R_1}\cdot\frac{s \,C_1R_1\left(s\,L_1 + R_2\right)}{ s \,C_1R_1\left(s\,L_1 + R_2\right) + R_1\left(1+s \,C_1 R_3\right) + \left(1+s \,C_1 R_3\right)\left(s\,L_1 + R_2\right)} \\\\ &=\frac{R_3}{R_1}\cdot\frac{s \,C_1R_1\left(s\,L_1 + R_2\right)}{\left(R_1 +R_3\right)C_1L_1\,s^2 + \left(L_1+C_1\left[R_1R_2+R_1R_3+R_2R_3\right]\right)\,s +R_1+R_2} \end{align*}$$

Do you think you can move towards a standard form from here?

Also, by this point, you should be able to see where I got my \$\omega_{_0}\$ from the comments. Just take the factor for \$s^2\$, \$\left(R_1 +R_3\right)C_1L_1\$, and divide that into the factor for \$s^0\$, \$R_1+R_2\$, to get \$\omega_{_0}^{\:2}=\frac{R_1+R_2}{\left(R_1 +R_3\right)C_1L_1}\$ or, in short, \$\omega_{_0}=\frac1{\sqrt{C_1L_1\frac{R_1 +R_3}{R_1 +R_2}}}\$. (And again, please refer to this page near where I discuss the fraction \$\frac{b_0}{b_2}\$.)

jonk
  • 77,876
  • 6
  • 77
  • 188
  • While speaking about the resonant frequency it may be helpful to remember how it is defined. And, therefore, I think the most direct way is to set the imaginary part of the transfer funtion equal to zero - and solve for wo. That means: The function must be real at w=wo. In the present case: When the numerator N is imaginary, the denominator D must also be imaginary (real part of D(s)=0) – LvW Apr 10 '22 at 10:04
6

The transfer function you need to derive can be undertaken in various ways and jonk offered a valid possibility. I am pushing the fast analytical circuits techniques or FACTs through my book on the subject because they naturally lead you to a low-entropy form where poles, zeroes and gains (if any) naturally show up in the expression. And this is what truly matters in the end, format the equation to make it deliver the information you need for the design: what is the resonant frequency, what elements affect it etc. This is the design-oriented approach or D-OA dear to Professor Middlebrook. It means it is needless to write an arm-long expression if its usage is intractable in the end.

In your case, for a second-order expression, you can easily identify the various elements which make the resonant frequency or the quality factor as long as you have all coefficients properly factored in the first place. And this is where the FACTs excel because they lead you straight there:

enter image description here

For higher-order networks, like your first one which is of 3rd order, you need to factor the polynomial form depending on which poles or zeroes dominate the response. You do this by examining the normalized time constants of each of the coefficients. If you see one of large value while the two others are quite small and not far away from each other, then you can say a pole dominates the low-frequency response while two poles can be grouped in the higher portion:

enter image description here

Have a look at this excellent excerpt from Fundamentals of Power Electronics where the authors discuss these time constants and how to rewrite an approximate expression (slide 45). It goes through the discussion of assessing the various time constants to, in the end, format the equation in a meaningful format to help you design your circuit.

Verbal Kint
  • 21,968
  • 1
  • 18
  • 55
  • I had to read the slides you posted to fully understand and appreciate your approach. This is wildly simpler than the approaches I’ve been taking. Thank you for this. – imthegman55 Apr 10 '22 at 12:26
  • If you want to discover the FACTs, you can check a seminar I posted on my web page. I taught the subject in 2016. The FACTs are very often the fastest and easiest way to go. What is truly unique with this technique is that you derive the transfer function via several steps. If, in the end, you realize the TF is wrong, then simply fix the guilty step instead of restarting from scratch if you apply the brute-force approach. Believe me, for complicated networks, it saved me more than once : ) – Verbal Kint Apr 10 '22 at 13:47