Magnetics design is hard. Bear with me as I walk through some of the considerations.
On the surface, it's actually fairly easy to figure out how many turns you need to get a given inductance on a given toroid.
First, check the datasheet for the core and see what the \$A_L\$ (inductance factor) is:
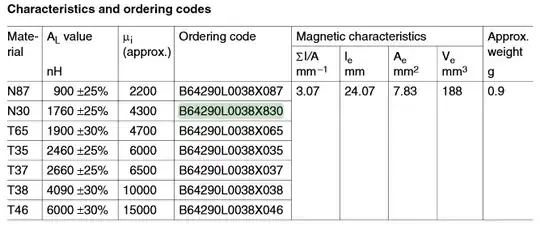
Your core's inductance factor is 1760nH +/- 25%.
The actual ratio that inductance factor stands for is:
\$ A_L = \dfrac{nH}{(turns)^2} \$
So, to get the number of turns you need, it's simple algebraic manipulation:
\$ turns = \sqrt{\dfrac{nH}{A_L}} = \sqrt{\dfrac{170000}{1760}} = 10\$
To figure out if your wire is going to fit, you need to consider the inside dimension of the toroid and figure out how many diameters of your wire can fit inside it.
Now the hard part.
To figure out whether or not the inductor is suitable for the application (i.e. will it saturate out) you need to know some things so you can calculate \$B_{max}\$:
- The operating frequency
- The expected peak-to-peak AC current
- Is there a DC component to the current
- The material characteristics
Number 4 is a biggie here. Why? The material for your choice of toroid is N30, which is suitable for frequencies from 10 to 400kHz according to the datasheet. Is this important?
That's the thing with inductors. The core material has a huge impact on what you can do with the part - it's not just the inductance. The core material dictates how much loss will be generated, at what flux density the core will saturate ... essentially everything.
You're not in a position to figure out the best number 4 unless you know number 1, 2 and 3. That means lots of calculations / predictions / simulations, and potentially lots of trial and error, before the magnetics are done 'right'.
So, will your 18AWG wire be OK for 10A? Most likely. The core? It depends on many things which you haven't specified in your question (like operating frequency, peak-to-peak ripple, etc.) so I cannot say for certain.
