Find Thevenin equivalent of given circuit with two voltage sources

Question

I have to find Thevenin equivalent circuit between M and N. So I understand that I have to get rid of R7, and find voltage of Vm and Vn, then Vth = Vm-Vn. But I don't understand how to calculate it. The two opposite voltage sources trip me out.

As for Rth, I calculate it as R8/R7/(R4+(R5/R6)) and get the result 3.75kohms.

I want to understand this problem, so any help would be appreciated.

Edit: So after simplifying the circuit, I calculate I1 = 0.5 mA and I2 = 0, then Vmn = 10 x 0.5 = 5 (V).

Is this correct?

Simplify the resistances on the right hand side and compute the current in the single loop. Then figure out the voltage difference across M,N. — copper.hat, Jan 12 '22 at 05:54
I might understand why you removed R7 first, but your calculation even without R7 is incorrect and you still need to add the R7 back to the circuit or you won't have a correct result. — Justme, Jan 12 '22 at 06:03
I assume you already have done these Thevenin equalent circuits previously. Its straight forward. Find Rth first by replacing all Sources to their equalent circuits. Find Voltage across M & N pins for Vth. — user19579, Jan 12 '22 at 06:12
By inspection the equivalent resistance is $10k || 10k || 15k$. — copper.hat, Jan 12 '22 at 06:16
If you do your computation correctly you will see that $I(V4)=0$. Then the Thevin equivalent voltage is straightforward to compute. — copper.hat, Jan 12 '22 at 06:25
There are lots of ways of solving these circuits. Learn how to combine two Thevenin equivalents in parallel. — copper.hat, Jan 12 '22 at 06:26
@NamHoang If $R_7$ is supposed to be part of the circuit within the black box that has just two nodes protruding, then your results are right. I get $V_{\text{TH}}=5:\text{V}$ (with M more positive than N) and $R{_\text{TH}}=3.75:\text{k}\Omega$. I didn't look over your process, though. — jonk, Jan 12 '22 at 07:47

score -1 · Answer 1 · answered Jan 12 '22 at 15:00

First, I will present a method that uses Mathematica to solve this problem. I know that this approach is not 'smart' but this method will work all the time, even when the circuit is way complicated than this one. In combination with the other answers, my answer is valuable.

Well, we are trying to analyze the following circuit:

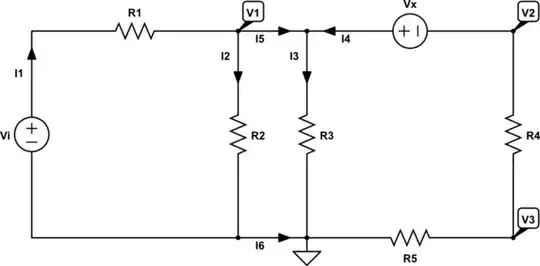
schematic

^{simulate this circuit – Schematic created using CircuitLab}

When we use and apply KCL, we can write the following set of equations:

$$ \begin{cases} \text{I}_1=\text{I}_2+\text{I}_5\\ \\ \text{I}_3=\text{I}_4+\text{I}_5\\ \\ \text{I}_4=\text{I}_3+\text{I}_6\\ \\ \text{I}_2=\text{I}_1+\text{I}_6 \end{cases}\tag1 $$

When we use and apply Ohm's law, we can write the following set of equations:

$$ \begin{cases} \text{I}_1=\frac{\text{V}_\text{i}-\text{V}_1}{\text{R}_1}\\ \\ \text{I}_2=\frac{\text{V}_1}{\text{R}_2}\\ \\ \text{I}_3=\frac{\text{V}_1}{\text{R}_3}\\ \\ \text{I}_4=\frac{\text{V}_3-\text{V}_2}{\text{R}_4}\\ \\ \text{I}_4=\frac{0-\text{V}_3}{\text{R}_5} \end{cases}\tag2 $$

Using \$(2)\$ and \$\text{V}_1-\text{V}_2=\text{V}_x\$ we can rewrite \$(1)\$ as follows:

$$ \begin{cases} \frac{\text{V}_\text{i}-\text{V}_1}{\text{R}_1}=\frac{\text{V}_1}{\text{R}_2}+\text{I}_5\\ \\ \frac{\text{V}_1}{\text{R}_3}=\frac{\text{V}_3-\text{V}_2}{\text{R}_4}+\text{I}_5\\ \\ \frac{\text{V}_3-\text{V}_2}{\text{R}_4}=\frac{\text{V}_1}{\text{R}_3}+\text{I}_6\\ \\ \frac{\text{V}_1}{\text{R}_2}=\frac{\text{V}_\text{i}-\text{V}_1}{\text{R}_1}+\text{I}_6\\ \\ \frac{\text{V}_1}{\text{R}_3}=\frac{0-\text{V}_3}{\text{R}_5}+\text{I}_5\\ \\ \frac{0-\text{V}_3}{\text{R}_5}=\frac{\text{V}_1}{\text{R}_3}+\text{I}_6\\ \\ \text{V}_1-\text{V}_2=\text{V}_x \end{cases}\tag3 $$

Now, we can set up a Mathematica-code to solve for all the voltages and currents:

In[1]:=Clear["Global`*"];
FullSimplify[
 Solve[{I1 == I2 + I5, I3 == I4 + I5, I4 == I3 + I6, I2 == I1 + I6, 
   I1 == (Vi - V1)/R1, I2 == V1/R2, I3 == V1/R3, I4 == (V3 - V2)/R4, 
   I4 == (0 - V3)/R5, V1 - V2 == Vx}, {I1, I2, I3, I4, I5, I6, V1, V2,
    V3}]]
Out[1]={{I1 -> (R3 (R4 + R5) Vi + R2 (R3 + R4 + R5) Vi - R2 R3 Vx)/(
   R1 R3 (R4 + R5) + R2 R3 (R4 + R5) + R1 R2 (R3 + R4 + R5)), 
  I2 -> (R3 ((R4 + R5) Vi + R1 Vx))/(
   R1 R3 (R4 + R5) + R2 R3 (R4 + R5) + R1 R2 (R3 + R4 + R5)), 
  I3 -> (R2 ((R4 + R5) Vi + R1 Vx))/(
   R1 R3 (R4 + R5) + R2 R3 (R4 + R5) + R1 R2 (R3 + R4 + R5)), 
  I4 -> (-R2 R3 Vi + R1 R3 Vx + R2 (R1 + R3) Vx)/(
   R1 R3 (R4 + R5) + R2 R3 (R4 + R5) + R1 R2 (R3 + R4 + R5)), 
  I5 -> (R2 (R3 + R4 + R5) Vi - (R1 + R2) R3 Vx)/(
   R1 R3 (R4 + R5) + R2 R3 (R4 + R5) + R1 R2 (R3 + R4 + R5)), 
  I6 -> (-R2 (R3 + R4 + R5) Vi + (R1 + R2) R3 Vx)/(
   R1 R3 (R4 + R5) + R2 R3 (R4 + R5) + R1 R2 (R3 + R4 + R5)), 
  V1 -> (R2 R3 ((R4 + R5) Vi + R1 Vx))/(
   R1 R3 (R4 + R5) + R2 R3 (R4 + R5) + R1 R2 (R3 + R4 + R5)), 
  V2 -> -(((R4 + R5) (-R2 R3 Vi + R1 R3 Vx + R2 (R1 + R3) Vx))/(
    R1 R3 (R4 + R5) + R2 R3 (R4 + R5) + R1 R2 (R3 + R4 + R5))), 
  V3 -> (R2 R3 R5 Vi - (R2 R3 + R1 (R2 + R3)) R5 Vx)/(
   R1 R3 (R4 + R5) + R2 R3 (R4 + R5) + R1 R2 (R3 + R4 + R5))}}

Now, we can find:

\$\text{V}_\text{th}\$ we get by finding \$\text{V}_1\$ and letting \$\text{R}_3\to\infty\$: $$\text{V}_\text{th}=\frac{\text{R}_2\left(\text{V}_\text{i}\left(\text{R}_4+\text{R}_5\right)+\text{V}_x\text{R}_1\right)}{\text{R}_1\left(\text{R}_2+\text{R}_4+\text{R}_5\right)+\text{R}_2\left(\text{R}_4+\text{R}_5\right)}\tag4$$
\$\text{I}_\text{th}\$ we get by finding \$\text{I}_3\$ and letting \$\text{R}_3\to0\$: $$\text{I}_\text{th}=\frac{\text{V}_\text{i}}{\text{R}_1}+\frac{\text{V}_x}{\text{R}_4+\text{R}_5}\tag5$$
\$\text{R}_\text{th}\$ we get by finding: $$\text{R}_\text{th}=\frac{\text{V}_\text{th}}{\text{I}_\text{th}}=\frac{\text{R}_1\text{R}_2\left(\text{R}_4+\text{R}_5\right)}{\text{R}_1\left(\text{R}_2+\text{R}_4+\text{R}_5\right)+\text{R}_2\left(\text{R}_4+\text{R}_5\right)}\tag6$$

Where I used the following Mathematica-codes:

In[2]:=FullSimplify[
 Limit[(R2 R3 ((R4 + R5) Vi + R1 Vx))/(
  R1 R3 (R4 + R5) + R2 R3 (R4 + R5) + R1 R2 (R3 + R4 + R5)), 
  R3 -> Infinity]]
Out[2]=FullSimplify[
 Limit[(R2 R3 ((R4 + R5) Vi + R1 Vx))/(
  R1 R3 (R4 + R5) + R2 R3 (R4 + R5) + R1 R2 (R3 + R4 + R5)), 
  R3 -> Infinity]]
In[3]:=FullSimplify[
 Limit[(R2 ((R4 + R5) Vi + R1 Vx))/(
  R1 R3 (R4 + R5) + R2 R3 (R4 + R5) + R1 R2 (R3 + R4 + R5)), R3 -> 0]]
Out[3]=Vi/R1 + Vx/(R4 + R5)
In[4]:=FullSimplify[%2/%3]
Out[4]=(R1 R2 (R4 + R5))/(R2 (R4 + R5) + R1 (R2 + R4 + R5))

So, using your values we get:

$$\text{V}_\text{th}=5\space\text{V}\tag7$$
$$\text{I}_\text{th}=\frac{1}{750}\approx0.00133333\space\text{A}\tag8$$
$$\text{R}_\text{th}=3750\space\Omega\tag9$$

Thank you so much for the very well-motivated downvote, I really appreciate it. — Jan Eerland, Jan 13 '22 at 09:33

Find Thevenin equivalent of given circuit with two voltage sources

1 Answers1