Simple series capacitance circuit

Question

I am a semi-retired Electrical Enginerr, and this question has me perplexed.

I don't need any info on capacitors, series calculations, transition effects, etc...

Here is the complete question but I'm just rusty on the charge distribution at equilibrium (and the energy) despite having read quite a few articles. That's what I'm mostly interested in help with.

Answer 1

The original charge in \$C_1\$ (when attached to the voltage) is now shared with the two previously discharged capacitors. In other words \$C_1\cdot V_0\$ becomes equal to \$C_{NEW}\cdot V_{NEW}\$.

• \$C_{NEW}\$ is the combined capacitance as seen from the top node to the bottom node.
• \$V_{NEW}\$ is new voltage as seen from the top node to the bottom node.

_{There is of course the mystical loss of energy due to infinite current flow for an infinitesimal period of time whan the discharged capacitors are attached but, the number of electrons that form the charge remain the same number as when C1 was originally charged (i.e. none of that energy mass conversion stuff).}

I'll also point out that the charge into the two new capacitors is the same (because they are in series) hence the voltages across each of them can be found using the basic Q = CV formula.

\$V_{C_2} + V_{C_3} = V_{NEW}\$ is also true.

As for whether all the capacitors are in series is down to how you look at the voltages. You can say they are all in series if you want. I prefer to think that C2 and C3 are in series then, together they become in parallel with C1. I think you should think that way in order to calculate V2.

Of course you can think of them in series because the charge that is redistributed (when C2 and C3 are added) flows equally through them all.

Answer 2

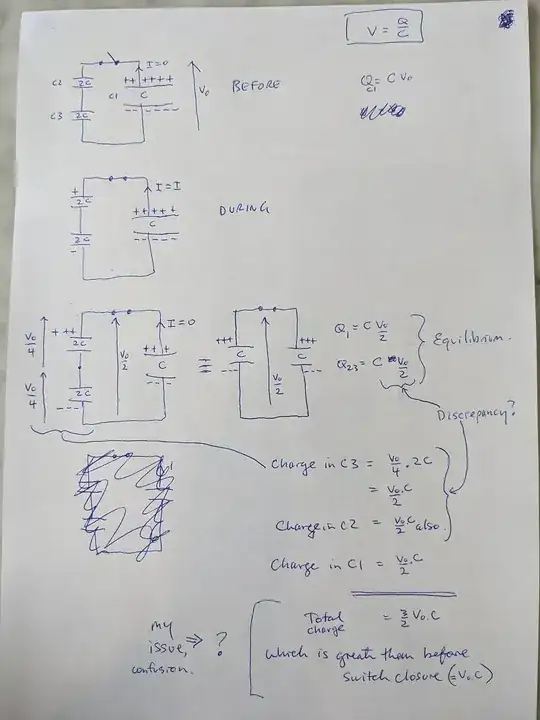
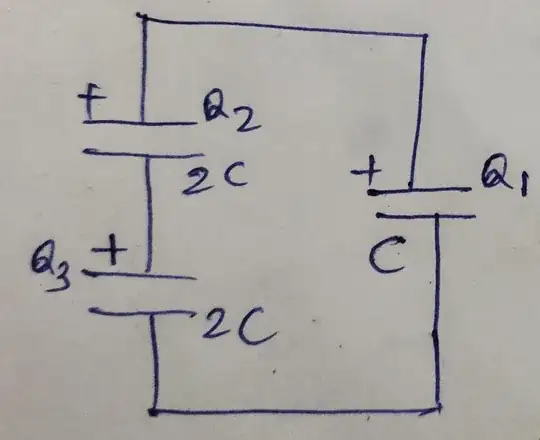
When the voltage source is replaced by 2 series caps the voltage across C1 will halve and so from Q=CV its charge will also halve.

The two other series caps in parallel to C1 will each have half the voltage across them, (half the voltage which is now across C1), but each of their capacitances is double that of C1. Therefore, from Q=CV, each of their charges is equal to that of C1's final charge.

So, as you suspected all three capacitors have equal charges but each is equal to half the original charge of C1.

I think you're having difficulty sorting this one out because your wrongly thinking that the total final sum of the charges of all three capacitors should be equal to C1's original charge but the redistribution of charge is caused by the flow of series current in the 3 capacitors and so the same current flows "through" the two series capacitors (which are in parallel to C1) carrying the charge to both of them.

EDIT

At the instant when the voltage source is replaced by two series capacitors a current starts to flow in an anti-clockwise direction around the circuit (talking about positive charge flow ie. conventional current). No conduction charge actually flows between the capacitor plates (apart from a tiny leakage current) but flows onto the uppermost plate of each of the two series capacitors and off of the lowermost plate of each of the two series capacitors. With regard to C1, the positive charge is flowing off (being removed from) its uppermost plate and flowing onto its lowermost plate. So the series current (flow of charge) is the same magnitude and direction at all points in the circuit.

This means that the series current is removing charge from C1 at exactly the same rate as it is adding charge to both C2 and C3.

Looking it another way, the rate of positive charge flow off the top of C1 and onto the top of C2 is the same as the rate of positive charge flow off of the bottom of C3 and on to the bottom of C1. Additionally the rate of charge flow off of the bottom of C2 and onto the top of C3 is the same.

And so the C1 discharge current is the same as the charge currents of both C2 and C3.

It may, at first seem a little difficult to understand how charge can flow off of the bottom of C2 and on to the top of C3 when the voltage at those point is identical but whilst this is happening, in collaboration with positive charge flowing onto the top plate of C2 and off of the bottom plate of C3, the voltage across both capacitors is increasing.

When considering capacitor charging it is good to remember that the currents in the leads of the capacitor always have the same magnitude but one flows in and one flows out. Then both currents change direction when discharging.

Answer 3

Let's consider the following charge configuration (in image)

from Charge conservation $$Q_1 + Q_2 =V_o C$$

$$-Q_1-Q_3=-V_o C$$

Using KVL

$$ -Q_1/C + Q_2/2C + Q_3/2C =0$$

again charge conservation

$$-Q_2 + Q_3 = 0 $$

Solving these three equations we get

$$Q_1 = Q_2 = Q_3 = V_o C/2$$