I have been attempting to port a modified version of the Yakopcic memristor from Python/MATLAB to LTspice but have been running into issues with the results not being the same, as shown in the following pictures.
In Python/MATLAB the memristor is simulated by using Euler's method to solve the IVP describing the device's internal state evolution.
MATLAB simulation result
[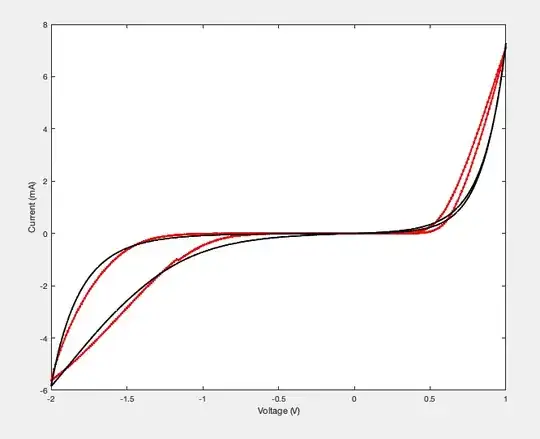 ]
]
I think that this answer may have put me on the right track (https://electronics.stackexchange.com/a/368910/294242) by pointing out that timing in the SPICE engine could lead to issues.
In fact, if I enlarge my timestep from dt=1/10000 to dt=1 in MATLAB/Python, I get the same exact result as in LTspice.
MATLAB simulation with dt=1 (the curve in black)
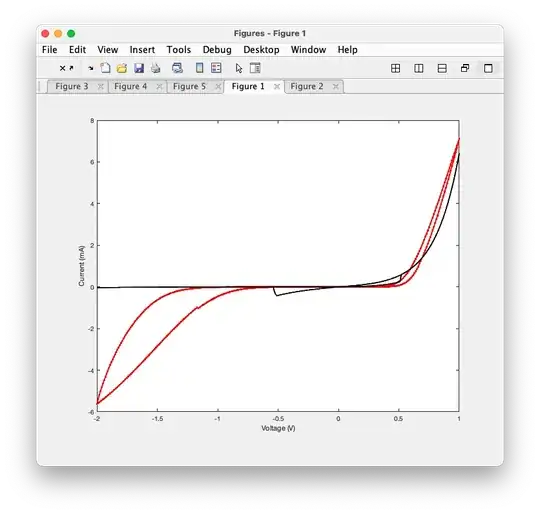
Is there any way to solve the issue I'm seeing? I have tried .tran 0 50s 0 {1/10000} to match dt=1/10000, but the results don't change.
* SPICE model for memristive devices
* Created by Chris Yakopcic
* Last Update: 8/9/2011
*
* Connections:
* TE - top electrode
* BE - bottom electrode
* XSV - External connection to plot state variable
* that is not used otherwise
.subckt MEM_YAKOPCIC TE BE XSV
- Fitting parameters to model different devices
- gmax_p, bmax_p, gmax_n, bmax_n: Parameters for OFF state IV relationship
- gmin_p, bmin_p, gmin_n, bmin_n: Parameters for OFF state IV relationship
- Vp, Vn: Pos. and neg. voltage thresholds
- Ap, An: Multiplier for SV motion intensity
- xp, xn: Points where SV motion is reduced
- alphap, alphan: Rate at which SV motion decays
- xo: Initial value of SV
- eta: SV direction relative to voltage
.param gmax_p=9e-5 bmax_p=4.96 gmax_n=1.7e-4 bmax_n=3.23
gmin_p=1.5e-5 bmin_p=6.91 gmin_n=4.4e-7 bmin_n=2.6
Ap=90 An=10
Vp=0.5 Vn=0.5
xp=0.1 xn=0.242
alphap=1 alphan=1
xo=0 eta=1
- Multiplicative functions to ensure zero state
- variable motion at memristor boundaries
.func wp(V) = xp/(1-xp) - V/(1-xp) + 1
.func wn(V) = V/xn
- Function G(V(t)) - Describes the device threshold
.func G(V) =
- IF(V > Vp,
Ap*(exp(V)-exp(Vp)),
IF(V < -Vn,
-An*(exp(-V)-exp(Vn)),
0 ) )
- Function F(V(t),x(t)) - Describes the SV motion
.func F(V1,V2) =
- IF(eta*V1 >= 0,
IF(V2 >= xp,
exp(-alphap*(V2-xp))*wp(V2),
1 ),
IF(V2 <= xn,
exp(alphan*(V2-xn))*wn(V2),
1 ) )
- IV Response - Hyperbolic sine due to MIM structure
.func IVRel(V1,V2) =
- IF(V1 >= 0,
gmax_p*sinh(bmax_p*V1)*V2 + gmin_p*sinh(bmin_p*V1)*(1-V2),
gmax_n*sinh(bmax_n*V1)*V2 + gmin_n*sinh(bmin_n*V1)*(1-V2)
)
- Circuit to determine state variable
- dx/dt = F(V(t),x(t))*G(V(t))
Cx XSV 0 {1}
.ic V(XSV) = xo
Gx 0 XSV value={etaF(V(TE,BE),V(XSV,0))G(V(TE,BE))}
- Current source for memristor IV response
Gm TE BE value = {IVRel(V(TE,BE),V(XSV,0))}
.ends MEM_YAKOPCIC
EDIT:
It turns out that the issue was not in the MATLAB to SPICE porting but rather in the original MATALB script itself. The MATLAB/Python script did not use a the same timestep as the real simulation.
I measured the experimental timestep and found it to be dt~=0.08s, so by using Euler with dt=1/10000 the MATLAB script was effectively simulating for only 60 ms, instead of the 50 s in the real experiment.
Scaling the Ap and An parameters to match the updated - much larger - timestep was enough to reproduce the experimental results.
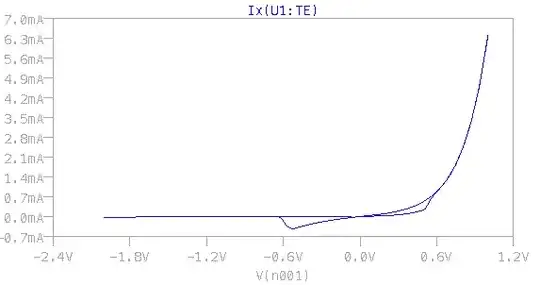
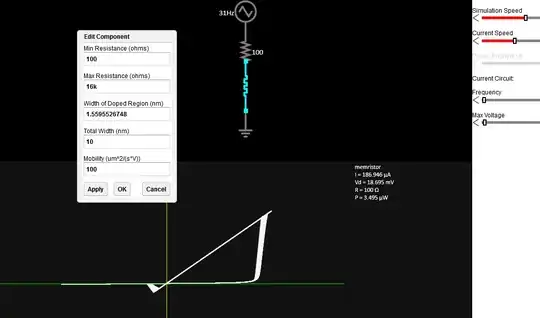
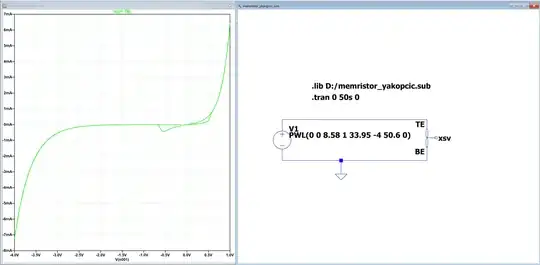
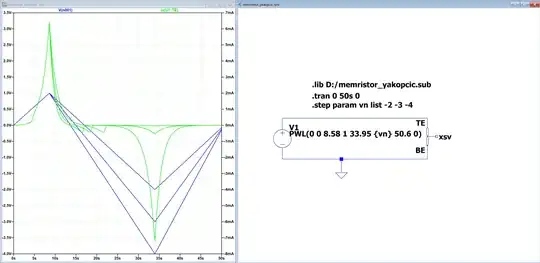

trapezoidal,modified trapezoidal, andGearintegration with no discernible outcomes. I also tried switching the solver fromNormaltoAlternate, again to no avail.I've also tried alternate solvers in Python (for ex.,
– Thomas Tiotto Aug 20 '21 at 14:41LSODA,RK4) and the results are the same as plain FE. (also, Yakopcic uses FE in his MATLAB simulations)