Impedance is defined as Z=U/I, so to define it you need two nets through which you define a current flowing and across which you define a voltage. "Looking into" is kind of a shorthand to talk about one net with respect to an implicitely defined local reference, with the added flexibility that the current out of the reference does not have to match the current into it:
 Imagine you look at the current going into your desired net. You would call that looking into that net.
Imagine you look at the current going into your desired net. You would call that looking into that net.
For example, the impedance looking into the base of a transistor is the impedance between the base and the emitter in a common emitter configuration (and yet the current into the base is much different from what flows out of the emitter). For a differential signal, it would be relative to the - terminal.
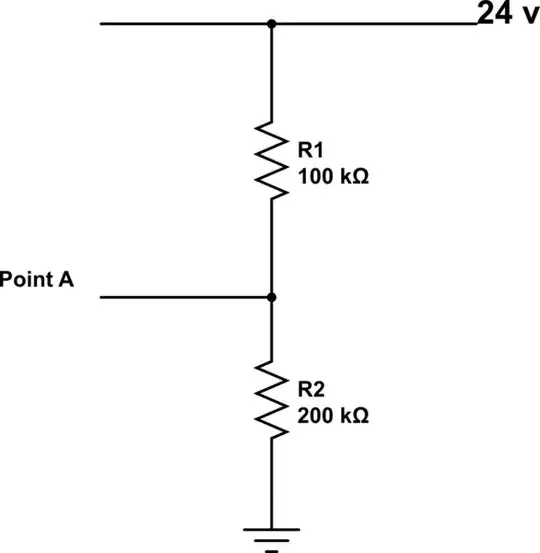
In your example, the impedance "looking into point A" is the impedance between A and GND, or 66.7kOhm following the base definition for impedance (open circuit voltage A-GND divided by short-circuit A-GND), but you can also consider that impedance is measured when all voltage sources are turned off - in this case 24V net shorted to GND => Z=R1//R2. Other tricks include looking for symmetry lines to find equipotential nets and short them to further simplify the circuit.
All of the above applies to steady-state/DC in linear circuits (i.e. only passives). You can do the same with dynamic signals and/or non-linear circuits by considering Z=dV/dI instead, as instantaneous/small-signal impedance around a DC bias point. It's basically like zooming in on the impedance plot (I=f(V)) that you would get "looking into" the net you want, until it's a line that's straight enough for your application: the system becomes by definition linear for small signals, and so you can solve the circuit one source ON at a time then sum the results.