....by eye-balling the peak-to-peak height of the sine wave on my 100 MHz
oscilloscope and multiplying by 2/sqrt(2)
That doesn't yield RMS. You need to divide by 2 to get peak then divide again by \$\sqrt2\$ to get RMS.
Is there a more accurate way (better than +- 10%) to measure milliVolt
Vrms, maybe using a simple circuit plus generic bench instruments
(DVM, scope, etc.).
You could make a peak detector circuit using a fast op-amp wired as an ideal rectifier but make sure you use a really fast op-amp (circa 500 MHz GBP) and a really fast reverse recovery diode like the BAS16 or 1N4148. The DC output will be the peak value and then you can use a voltage divider to produce the RMS. That then makes it a peak detector that is useful.
Begin with a precision rectifier (circuit from from wiki): -

I've built one that was good for 40 MHz using a fast op-amp and fast diode. You'll need to add a small capacitor on the output to 0 volts (circa 100 pF) to "catch" the peak and, maybe a parallel resistor with the capacitor to slowly discharge the peak after the event has gone.
If I remember correctly I actually used a fast comparator (MAX999) instead of an op-amp but, bear in mind that the MAX999 has input hysteresis of a few milli-volts that will create a tiny error however, it does slightly simplify the precision rectifier to this: -
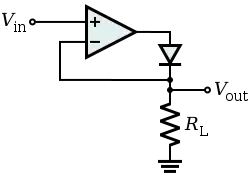
If you make \$R_L\$ around 10 kΩ and use a parallel 100 pF capacitor, you get a time constant of 1 μs which is good enough as a peak detector for 30 MHz but may be a bit sloppy for 3 MHz so, make the output capacitor more like 1 nF.

