Discrete time decimation bandwidth expansion

Question

I have been reading about discrete time decimation in Signal and Systems by A.Oppenheim. The decimation process expands/scales the bandwidth of the original non-decimated signal by N, I have a hard time visualizing/reconciling this because of the relationship X[e^jw]= X[e^jw/N]. It seems as though if you divide w by N the bandwidth would be getting more compacted, not spread out. Can someone please point me in the error of my ways,

Appreciated.

It's not clear to me what you are asking. But is it related to this? — jonk, May 17 '21 at 18:45
$f(x/2)$ is a "wider signal" than the original $f(x)$. Is that what you are asking? — AJN, May 18 '21 at 01:57

score 0 · Answer 1 · answered May 17 '21 at 18:55

In the case of FIRs the frequency response is:

$$H[k]=\sum_{n=0}^{N-1}{h[n]\mathrm{e}^{-j2\pi kn/N}} \tag{1}$$

therefore for each of the coefficients of length \$N\$ there will be a complex exponential. Decimation by \$2\$ means every other coefficient is rejected, resulting in only half of the terms of \$h[n]\$ being summed, therefore the frequency response will have half the magnitude. And since the exponentials are also halvened in number the spectrum is now twice the width:

$$G[k]=\sum_{n=0,n=2n}^{N-1}{g[n/2]\mathrm{e}^{-j\pi kn/N}} \tag{2}$$

Think of it in terms of basic functions: \$\sin(x)\$ has one period between \$[0,2\pi]\$, while \$\sin(x/2)\$ will only have one half.

If, OTOH, you take the original filter and nullify every other sample, it would be the same as taking the decimated impulse response and upsample it by \$2\$. Therefore the response now will be:

$$F[k]=\sum_{n=0,n=2n}^{N-1}{f[n]\mathrm{e}^{-j2\pi kn/N}}$$

Here \$f[n]\$ will have the same number of coefficients as the decimated one, \$g[n]\$, the same halvened number of complex exponentials, but the full length of the original filter, \$h[n]\$. For every other coefficient the value will be zero, hence the \$n=2n\$. This means that the spectrum is squished, and its magnitude will still be only half of \$h[n]\$.

You can confirm this in Octave, for example:

h=200/512*sinc(200/512*[-20:20]);
g=downsample(h,2);
f=upsample(g,2);
subplot(1,2,1);
stem(h), hold on, stem(g), hold on, stem(f), hold off;
N=1024;
H=fft(h,N);
G=fft(g,N);
F=fft(f,N);
subplot(1,2,2);
plot(abs(H),"",abs(G),"",abs(F))

test

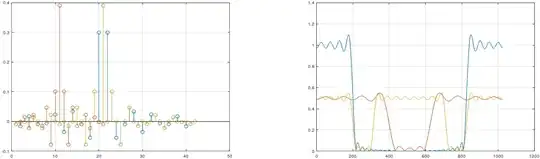
To the left, \$h[n]\$ is blue, \$g[n]\$ is red, and \$f[n]\$ is yellow, while to the right their frequency responses preserve their colours. Therefore \$H[k]\$ is blue and is the reference, \$G[k]\$ is red and is half the magnitude, twice the bandwidth, while \$F[k]\$ is yellow and is again only half of \$H[k]\$.

Discrete time decimation bandwidth expansion

1 Answers1