In a sine/cosine encoder, position information is encoded in two 90 degree phase shifted sinusoidal signals. Typically, the approach to decode this information is by generating a coarse quadrature signal and sum a finer position information, interpolated through the arctan function:
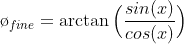
My question relates to this implementation. Since both signals originate from the same source, I assume that the cosine signal does not encode any extra information that can be extracted purely from the sine signal. Although they are both generated from the same source, the cosine signal will have phase, gain and offset errors in relation to the sine signal, which limit the accuracy of the previous calculation. So why are both signals used? To obtain the fine position information, can't the arctan function be applied to an original signal, for instance the sine wave, and a "virtual" 90 degree offset signal, cosine, generated from this sine wave, therefore eliminating these sources of error?
