MOSFET switching times due to dynamic gate current

Question

I'm having difficulties in understanding this statement from "The Art of Electronics 3rd Edition".
I don't understend how they estimated the MOSFET's switching time using the gate current and the feedback capacitance.

Here is the quote:

As another example, imagine switching a 5 amp highvoltage load with a power MOSFET (there aren’t any highpower JFETs), in the style of Figure 3.50. One might naively assume that the gate could be driven from a digital logic output with low current-sourcing capability, for example the so-called 4000-series CMOS logic, which can supply an output current of the order of 1mA with a swing from ground to +10V. In fact, such a circuit would be a disaster, because 1mA of gate drive into the 200 pF average feedback capacitance of the IRF740 would stretch the output switching speed to a leisurely 50μs.

Figure 3.50:

Thanks.

Answer 1

There is a factual error here, but it's somewhat beside the point, and not inconsistent with data presented in the book (there's just a gap in those data where they would be relevant to this problem).

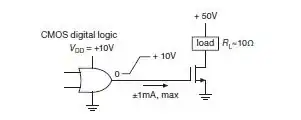
Since the load is 50V and the gate drive is 10V, the change in voltage across C_rss is 60V. 200pF at 60V is 12nC, and 12nC at 1mA is 12µs -- in the right ballpark, at least.

From the footnote p.164 (AoE3 reprint with corrections 2015),

⁵⁴ Out model is unacceptably crude, because feedback capacitance varies rapidly with drain voltage (see §3.5.4A). It's OK to use a constant value for feedback capacitance C_rss for small-signal calculations; but for a switching application like this, you need to go to the datasheet for values of gate charge, which take into account the nonlinear behavior of the capcaitances. In this example the datasheet specifies Q_G ≈ 40nC of gate charge, producing a switching time of t = Q_G/i = 40µs at a (dynamic) drive current i of 1mA.

We notice a conflation of terms: the paragraph describes output switching speed, i.e. V_DS swing, which depends largely on Q_GD, while the footnote uses Q_G, giving the gate voltage switching speed. The numbers don't match, anyway; I suspect the 50µs might be a typo for 40.

One of the downsides to AoE's conversational style of presentation, is the sparsity of formulas, rigorous definitions, specific mechanical relationships, etc.. While it can be (and has been, and is being!) used as a textbook, it is but a starting point for a curriculum, and either much coursework is required (i.e. write your own lectures), or use the teaching supplements they've written, to cover those aspects. As a result, looking at the book alone, we don't really have enough material in this section, or in general, to demonstrate inconsistency. (Which is a bit disappointing for a book of this scale and prestige; but just as well, that's a lot to ask from one book, and if the authors were to write it for every possible use and audience, it would be exponentially larger -- and consequently much less useful to any given audience or purpose. So, they've chosen to keep it in a specific style and tone they find most appealing.)

At best, we can intuit what's being asked for, i.e. Miller effect (see §2.4.5B), and suppose that, between initial and final conditions, the above total change must have occurred, and since we're given an average/effective capacitance, we should use that, and the voltages indicated. Why the text doesn't use the same figure (12µs), or comments on Q_G, I don't know.

---

As for the omission I alluded to at the top -- CD4000 family logic is rated for around 1mA output at 10V, it's true, but this is not a characteristic.

Specifically, CD4011B is characterized as 0.9 to 2.6mA or more (depending on temperature and bounding) at V_DD = 10V, for a rated voltage drop (from rails) of 0.5V. This gives a solidly logic-high or logic-low voltage, under a rated load, suitable for digital/hybrid design use.

Additional figures specify the output characteristic: in fact, at V_DD = 10V, typical maximum sink and source currents are +15 and -20mA; and the impedance is not constant-current, but gently curved, enough that we can take it as an average resistance: suppose we take the currents at V_DD/2 and average them: about 15 and 12, or 13.5mA together, and at 5V drop is 370Ω.

We can take this as an RC equivalent circuit with the equivalent gate capacitance, and get gate switching time. For 40nC at 10V, the equivalent is 4nF (C = Q/V), and the time constant is 1.48µs. 10-90% switching time is about 2.2 RC or 3.2µs.

Finally, we note that the effective gate-drain capacitance, gate referred, is a fraction of the total and therefore output transition time will be a similar fraction of the total gate transition time. That is, for Q_GD of 21nC, out of a total 43nC, we expect 49% or 1.56µs drain transition time.

(Incidentally, the datasheets only give maximum: 32nC Q_GD, 63nC total. It's not clear where their "typical" figures came from; they might've even measured a selection of parts... which makes Table 3.4 even more impressive.)

Because of all the nonlinearities around, even this many digits of accuracy is a vast overstatement; on the gate side, C_iss increases dramatically between off and on states, so the settling-out to V_DD at turn-on takes much longer than the settling-out to 0V at turn-off. Conversely, we have lower (incremental) resistance from the driver when it's closer to the supply rails -- remember the typical rating of 2.6mA at 0.5V drop, or 192Ω R_DS(on), which will speed things up a bit as they settle into place. On the drain side, we don't know exactly where the Miller plateau will fall: if it occurs at low voltage for example, then relatively high current is sourced into it at turn-on, and relatively low current sunk out at turn-off. Plateau voltage depends on V_GS(th) and I_D, i.e. device and load parameters, at the very least.

(There could also be source inductance (shared between gate and drain circuits), which effectively shifts the Miller step upwards during turn-on, and downward at turn-off. It would be rather high inductance to cause problems at this rate of switching, for this scenario -- it's only doing 5A load, and say a change of 1V, for an average rate of 5A/1.56µs, is L_s ≈ 0.3µH. Which would be rather a lot of wire length -- about a foot, and would likely come with other problems like potential for oscillation, or EMI.)

---

Anyway, I think the section in question is somewhat throwaway, as it doesn't connect strongly with surrounding matter, and is more the point of, bringing up the idea to get you thinking about gate current requirements and switching speeds. It's odd that it's not very consistent, nor well motivated or connected, so does seem like a section that's evaded editing for a bit.

On the upside, if you feel there is a factual or other error, or just have questions or comments about it, the authors can be reached by e-mail, and are always interested in corrections. Just make sure to check carefully that you've actually found an error, do your due diligence, avoid wasting their time, etc. :)

Also on that note, given this is a 2015 version, it may have been corrected since. Though I don't see the page number in the errata at this time.

Answer 2

Hmmm. My math doesn't agree with AoE. Assume that the MOSFET gate is a lumped, constant capacitance of 200pF. For a capacitor,

\$i = C\dfrac{dV}{dt}\$

so

\$\dfrac{dV}{dt} = \dfrac{i}{C}\$

If the current is 1mA then \$\dfrac{dV}{dt}\$ is \$5 \text{V}/\mu\text{s}\$, so it would take \$2 \mu\text{s}\$ to switch the gate voltage by 10V.

Maybe I am missing some context?