I struggled to understand the given answers and comments, and kept redirecting myself but all to wrong directions. Now that I think I have it figured out, the question really should be asking - what is \$ \Delta f \$?
A resistor by itself generates noise from random movement of electrons inside that resistor. Without noise, the resistor measures at 0V flat. With noise, it measures at some random voltage values fluctuating above and below 0V. Noise, like signals, is a waveform of voltage (or current). Like any other waveform, periodic or aperiodic, noise is a superposition of sinusoids varying in frequency and amplitude.
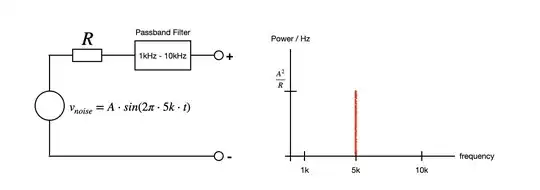
If we model the noise generated by a resistor as a voltage source \$ v_{noise} \$, and that we (unrealistically) assume the noise to be a single sinusoid that has frequency within the bandwidth of a passband filter, we can measure the power of that noise (or equivalently, the power of that single frequency). I think the graph (Power/Hz vs. Frequency) is what they call the Power Spectral Density (PSD).
Johnson Noise (or Johnson-Nyquist, Nyquist, Thermal, White Noise), as it turns out, generates an average \$ k_bT \$ watt of power for each and every constituent frequency of that noise. Thermal noise, as a random waveform, is composed of an infinite number (hence, a continuum) of sinusoids, each having a constant power of \$ k_bT \$. That explains the straight flat line valued at \$ k_bT \$ across the entire spectrum to infinity.
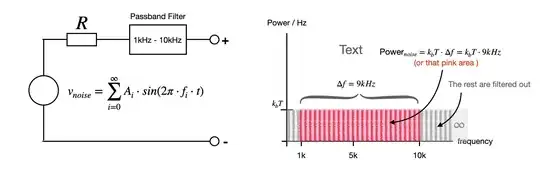
The passband filter let through the set of frequencies between 1k-10kHz and filters the rest of the noise frequencies to ground. \$ \Delta f \$ is the bandwidth of the filter, and the area is dimensionally the power of noise! The wider the bandwidth, the bigger the noise power.
If I remove the passband filter, the noise will now be filtered by the bandwidth of my oscilloscope and the intrinsic/parasitic serial or parallel capacitance or inductance (which also acts like filters) of the resistor. Thus in reality, there's always a bandwidth existed somewhere to prevent you from collecting an infinite amount of noise power, and that the finite power is a function of the bandwidth \$ \Delta f \$.