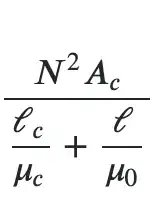Yes the inductance will be much much lower than a closed toroid. However, there is still some benefit from the high permeability of the core material.
If you are interested in calculating the flux density (and therefore inductance) due to the magnetization of a particular coil, then I would suggest taking a look at this paper.
Kaverine, Evgueni & Palud, Sebastien & Colombel, Franck & Himdi, M.. (2017). Investigation on an Effective Magnetic Permeability of the Rod-Shaped Ferrites. Progress In Electromagnetics Research Letters. 65. 43-48. 10.2528/PIERL16110203.
Since we already know that
$$L=\frac{N^2\mu_0\mu_rA_e}{l}$$
The effective relative permeability of the rod comes from its geometry and the permeability of the core material (again see paper above). I would recommend the simple calculation based on empirical data
$$\mu_{rod}=\frac{\mu_{core}}{1+0.84\left(\cfrac{d}{l}\right)^{1.7}(\mu_{core}-1)}$$