Electric field
Lets consider a simpler example. A spherical surface of radius \$a\$ with uniformly distributed charge \$Q\$ on it. Let the sphere be centred at the origin for convenience. Let the space be vacuum. The charge density is
\$\frac{Q}{4\pi\ a^2} \mathrm{\frac{coulomb}{m^2}}\$.
Electric field E is given by
\$
E = \begin{cases}
0, & r < a & \text{inside}\\
\frac{Q}{4\pi\varepsilon_0\ r^2} & r > a & \text{outside}\\
? & r=a & \text{on the sphere}
\end{cases}
\$
The question as I have understood is: "Where to place the equals symbol ?".
Clearly, the case with equals symbol on both cases
1
\$
E = \begin{cases}
0, & r \leq a \\
\frac{Q}{4\pi\varepsilon_0\ r^2} & r \geq a
\end{cases}
\$
is wrong since E is defined as 0 as well as \$\frac{Q}{4\pi\varepsilon_0\ a^2} \neq 0\$ for the case \$r = a\$. Electric field can't have two different values at the same location at the same time (in classical mechanics?). So this option is ruled out.
In other words, for discontinuous functions like the one shown here for electric fields, you cannot put the equals sign in both places at the same time since the values calculated from both equations are different and a field cannot have two values at same time at same location.
2
Another option is not to put the equals sign in either case. This is not wrong, but E is left undefined at \$r=a\$. In certain scenarios, this is okay. For example, to find the potential V, we need to integrate E from \$r = \infty\$ to \$r=\mathrm{some value}\$. Even if the value of E is undefined at \$r=a\$, we can still perform the integration if the value of E at \$r=a\$ is finite as \$\int_{a^+}^{a^-}E(r) dr = 0\$ if \$E(a)<\infty\$.
Two other options are either
3
\$
E = \begin{cases}
0, & r \leq a \\
\frac{Q}{4\pi\varepsilon_0\ r^2} & r > a
\end{cases}
\$
or
4
\$
E = \begin{cases}
0, & r < a \\
\frac{Q}{4\pi\varepsilon_0\ r^2} & r \geq a
\end{cases}
\$
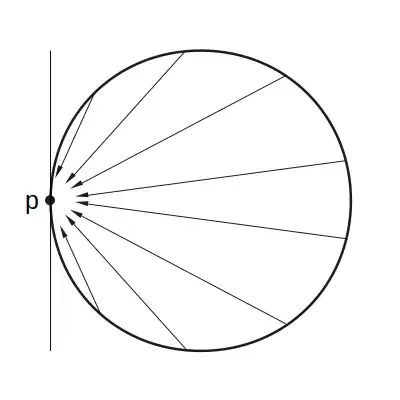
To see if #3 or #4 is more appropriate, consider the case \$r=a\$. To see if the electric field is zero consider placing a test charge at \$r=a\$ and find the force acting on it. From the below figure, we can see that the forces from all parts of the figure are pointing right-to-left and there is no left-to-right force to cancel them. So the Electric field is not zero. That rules out option #3 also. We have not established if the field is \$\frac{Q}{4\pi\varepsilon_0\ r^2}\$. If we can do that, then option #4 is the correct way to place the equals sign. You can also note that this is followed in the second example you have supplied (for \$a\$, but for \$b\$ there is no equals sign at all).
Potential
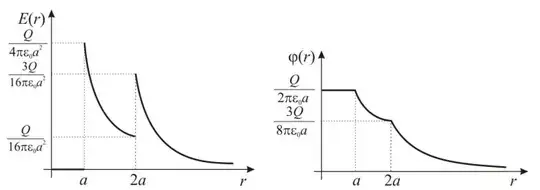
For V there is not such confusion since the plot of V is a continuous line and hence even if we put equals sign on all inequalities, the result from the different equations are the same for this particular example. So, for potential V, #1 (equals sign in both places) is also correct.


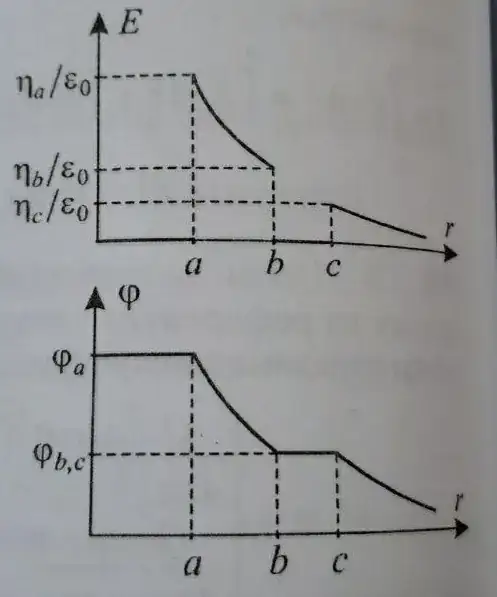

bandc. There is a mismatch between the figures and the numbered lists above it. – AJN Aug 04 '20 at 07:32