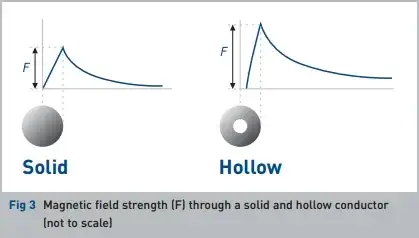
Question : An infinitely long, very thin cylindrical conducting tube of radius b carries a uniform surface current Js = azJs(A/m). Find B everywhere.
When r<b, it says that "In condition flux density of cylindrical conducting tube is 0 because the cylindrical tube has no internal surface. So when the condition the flux density is 0."
: Why there is no internal surface?