Filter passband amplitude ripple and group delay ripple (group delay variation)

Question

Are they completely independent? or does one lead at least partially to the other?

Answer 1

Whenever you have any complex function that is analytic in the upper half-plane (why this matters will become clear) you can relate uniquely and exactly the complex and real parts of the function through what is called the Kramers-Kronig relations.

Why does this matter? Well, it turns out that any causal system, which is a system where the output depends only on past inputs (which any real-world system is unless you invent time-travel), is described with a complex function that is analytic in the upper half-plane.

This means that if we only know the exact amplitude behavior of your system (which is the real part), we can calculate what the imaginary (phase/group delay) part must be. In other words, yes, there is a strict relationship between amplitude and group delay ripple of a filter.

This is also why it is impossible too make a filter (or any system really) that implements an arbitrary phase and amplitude response - if we pick one, we have indirectly also picked the other.

This is sometimes used to calculate the loss of very, very low-loss materials, because it is much easier (but still really hard) to measure their phase behavior (which would be the permittivity/permeability) than it is to measure their loss. We can then calculate the loss from the phase behavior.

Answer 2

In addition to what @Joren Vaes said, it may be easier to think in terms of H(s) being the (complex) transfer function, the phase being the argument of H(s), and the group delay as the negative derivative of the phase. The phase delay is the negative phase divided by frequency. Random example with a 2nd order Chebyshev with ~1.25dB ripple:

$$\begin{align} H(s)&=\frac{1}{s^2+s+1} \\ H(j\omega)&=\frac{1}{-\omega^2+j\omega+1} \\ \Re\{H(j\omega)\}&=\frac{1-\omega^2}{\omega^4-\omega^2+1}\qquad\Im\{H(j\omega)\}=-\frac{\omega}{\omega^4-\omega^2+1} \\ \Phi(\omega)&=\arctan{\frac{\Im\{H(j\omega)\}}{\Re\{H(j\omega)\}}}=\arctan{-\frac{\omega}{1-\omega^2}} \\ gd(\omega)&=-\frac{\mathrm{d}\Phi(\omega)}{\mathrm{d}\omega}=\frac{\omega^2+1}{\omega^4-\omega^2+1} \\ pd(\omega)&=-\frac{\Phi\bigl(H(j\omega)\bigr)}{\omega} \\ \end{align}$$

So, as you can see, the group and phase delay come directly from the transfer function.

---

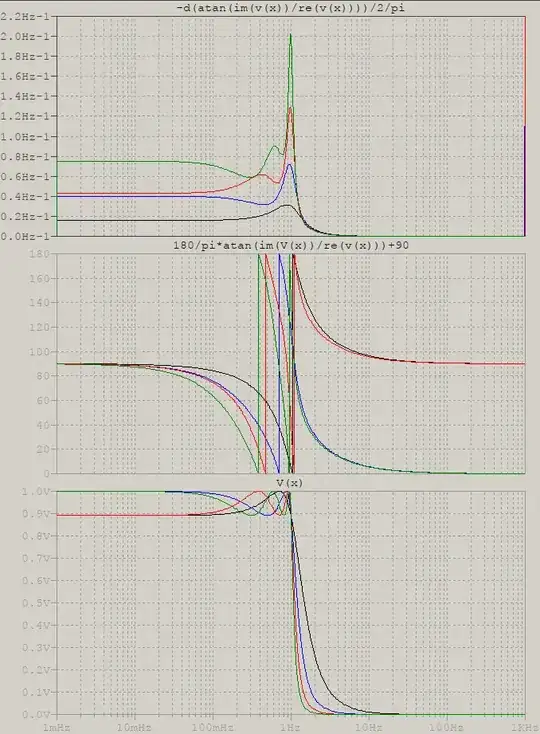
I showed how phase and group/phase delay are directly derived from the transfer function. That means that, no matter how the t.f. is, the phase and delay will inherit, in full. I'm not sure what isn't clear, or what more evidence is there needed that there isn't some half-baked relation, but a full, direct relation between these, but maybe a picture will say more than words can? Here is how the magnitude, phase, and group delay vary for a 1 Hz Chebyshev filter with orders from 2 to 5 -- it can be clearly seen that as the ripples and the transition widths increase, so do the phase and group delays change:

Answer 3

Intuitively, you know that for a simple RLC filter that the higher Q, by definition, reduces the -3dB bandwidth for changes in both amplitude and π phase shift per LC pair. Thus the rate of change per Hz for dB amplitude and group delay = dΦ/df are affected by damping factor or 1/Q thus the ripple of both.

You may learn all the dozen or more classic filter types, that tradeoff these characteristics between Amplitude vs Group Delay vs jitter ripple by controlling the ratio of real/reactive elliptical vs circular shape of Root Lotus plots.

Credit to https://en.wikipedia.org/wiki/Minimum_phase

also read https://en.wikipedia.org/wiki/Kramers%E2%80%93Kronig_relations#Magnitude_(gain)%E2%80%93phase_relation