Why am I getting different flux densities?

Question

I am trying to find the flux density at the top of the core. The current is known to be 2.5 A, the relative permeability of the core is known to be 800 H/m, and the flux is known to be 0.005 Wb.

When using the following equation: B_top = φ/A_top = 0.005/0.0075, I get B_top = 0.67 T.

However, when using the following equation: B_top = μNi/l = 800(4π)(10^-7)(500)(2.5)/0.275, I get B_top = 4.57 T.

Is there a reason why I'm getting two different answers from the two equations?

Answer 1

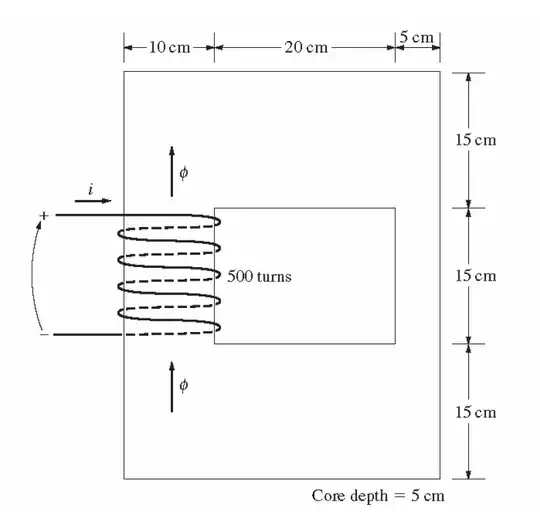
The H-field is: -

$$\dfrac{MMF}{\ell_e}$$

• Where MMF (magneto motive force) is amps x turns = 2.5 x 500 = 1250 At
• Where \$\ell_e\$ (effective mean length of core)
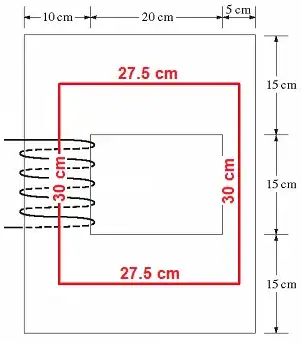
• The top and bottom mean length is that length through the centre line i.e. 5 cm + 20 cm + 2.5 cm = 0.275 m.
• The vertical mean length is 7.5 cm + 15 cm + 7.5 cm = 0.3 m.
• This means \$\ell_e\$ (the effective mean length of the core) is 1.15 metres: -

Hence, the H-field is 1250 / 1.15 = 1086.96 At/m

Given that \$\mu_r\$ is stated to be 800 (and note that \$\mu_r\$ is a relative quantity and is dimensionless i.e. not defined in henries per metre), it's absolute (or effective) permeability (\$\mu_e\$) is: -

$$4\cdot\pi\times 10^{-7}\times 800 = 1.0053\times 10^{-3}$$

Knowing that B (flux density) = H-field x \$\mu_e\$, B = 1.093 teslas.

This is the overall average flux density and is not tied in with one limb of the core or the other. For instance, the flux density for the upper section (as stated in the question as 0.005 webers) and, this translates to a B-field of 0.6667 teslas (0.005/Area = 0.005/0.0075). But the calculated flux density for the right-hand vertical section is 0.005/0.0025 = 2 teslas. Hence, my calculated value (1.093 teslas) is about right. I mean you could do this the harder way and calculate reluctances for each core limb but I'm sure you'll get to 1.093 teslas as the average.

So, this doesn't tally with your calculated value of 4.57 teslas. However, it looks like you might have used 0.275 m for the mean length whereas I used 1.15 m. That looks like it would make your answer the same as my average value for \$B\$.

Is there a reason why I'm getting two different answers from the two equations?

Go through my procedure carefully to double check my numbers first. Then, it might be that one error is in the way you calculated mean core length and, there will be a difference in flux densities due to the differing thickness of each side compared to top and bottom. If the stated flux of 0.005 webers is to be believed, you'll get different \$B\$ values on each limb.