I can't figure out why drain voltage is rectangular in the following circuit:
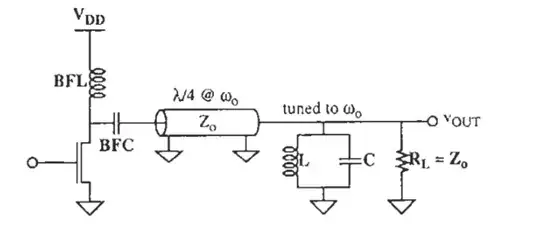
I tried this:
$$ V_{ds}=V_{DD}-I_{fund}R_lsin(\omega_0t)-I^{(2)}Z_{in}^{(2)}sin(2\omega_0t)-I^{(3)}Z_{in}^{(3)}sin(3\omega_0t)... $$ $$ I^{(k)}= \int i_{d}sin(k\omega_0t)dt $$ $$ Z_{in}^{(2k)}=0\\Z_{in}^{(2k+1)}=\infty\rightarrow I^{(2k+1)}=0 $$ $$ \rightarrow V_{ds}=V_{DD}-R_lI_{fund}sin(\omega_0t) $$ So the output I get is sinusoid but the reference I studied states it is rectangular. Would anyone please help me with this?
Edit: The transistor is assumed to act as switch.