The problem here was when I tried to counter check my answer using algebra and the two techniques above I got three different outputs all together.
The code:
G1=tf([0 1],[1 10]);
G2=tf([0 1],[1 1]);
G3=tf([1 0 1],[1 4 4]);
G4=tf([1 1],[1 6]);
H1=tf([1 1],[1 2]);
H2=tf([0 2],[0 1]);
H3=tf([0 1],[0 1]);
k=tf([2 12],[1 1]); % H2/G4 - I moved G4 before H2
feedback((series((feedback((series((feedback((series(G3,G4)),H1,+1)),G2)),k,-1)),G1)),H3,-1)
%me checking for errors
syms s;
g1=1/(s+10);
g2=1/(s+1);
g3=((s^2)+1)/((s^2)+4*s+4);
g4=(s+1)/(s+6);
h1=(s+1)/(s+2);
h2=2;
h3=1;
simplify(g3g4)
series(G3,G4)
simplify((g3g4)/(1-(g3g4h1))) % so far so good
feedback((series(G3,G4)),H1,+1)
simplify((g2g3g4)/(1-(g3g4h1)))
series((feedback((series(G3,G4)),H1,+1)),G2) %and here's where it fell apart
%me trying another approach
G1=tf([0 1],[1 10]);
G2=tf([0 1],[1 1]);
G3=tf([1 0 1],[1 4 4]);
G4=tf([1 1],[1 6]);
H1=tf([1 1],[1 2]);
H2=tf([0 2],[0 1]);
H3=tf([0 1],[0 1]);
R=tf([0 1],[0 1]);
t1=append(G1,G2,G3,G4,H1,H2,H3,R);
q=[1 8 -7;2 1 -6;3 2 5;4 3 0 ;5 4 0 ;6 3 0 ;7 4 0;];
input= 8;
output=4;
ts=connect(t1,q,input,output);
tf(ts) % It gave a whole new different answer
Can anyone point out where I went wrong?

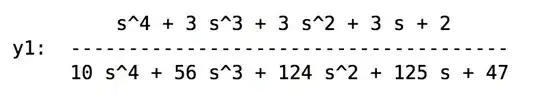

series(G3,G4) it starts out good
feedback((series(G3,G4)),H1,+1) it works fine here
series((feedback((series(G3,G4)),H1,+1)),G2) why does it freak out here?
further more it freaks out even more when I use the append command format
– PHO BOSS Jun 14 '19 at 22:37