Is the transfer function for the given RC network right?

Question

For the question

I arrived at the following answer (I have assumed V1 btw)

Is my solution right? I just have a big doubt if whether I can use the voltage division rule at point A when there is an RC network after it.

Answer 1

This exercise is a classic and you can see that applying brute-force algebra leads to a complex expression, difficult to factor. Furthermore, you can make mistake as you did. First, assign proper labels to each of the components, \$R_1\$, \$C_1\$ etc. It is important for the correct arrangements of results. If you want to solve this transfer function the hard way, transform the first stage with an equivalent Thévenin generator taken across the first capacitor. Its output impedance is \$Z_{th}(s)=\frac{1}{sC_1}||R_1\$ while the voltage is \$V_{th}(s)=\frac{\frac{1}{sC_1}}{\frac{1}{sC_1}+R_1}\$. Then, solve a resistive divider implying \$R_{th}\$, \$R_2\$ and \$C_2\$. Good luck with that!

The easiest and fastest way is to apply the fast analytical techniques or FACTs. When dealing with passive or active elements, they can't be beaten. First, consider the dc case, \$s=0\$. What is the gain when all caps are open-circuited? It is 1 in absence of a loading resistance: \$H_0=1\$.

Then, remove the capacitors while you set \$V_{in}\$ to 0 V: replace it by a short circuit and "look" into each capacitor's connecting terminals to determine the resistance you see. This resistance multiplied by the considered capacitor forms a time constant \$\tau=RC\$, the basis of the FACTs. You do that as illustrated in the below drawings and you have \$b_1=\tau_1+\tau_2\$ in a few seconds.

Then, select one of the caps and set it in its high-frequency state (a short circuit) then "look" into the terminals of the second cap. Combine this new time constant with one that you have already determined (\$\tau_1\$ for instance) and you have the second-order term: \$b_2=\tau_1\tau_{12}\$.

Once done, you can write the denominator \$D(s)=1+sb_1+s^2b_2\$ and express the transfer function as in below Mathcad sheet. The equation as it is is difficult to use, you have no insight in what is does. Apply the low-\$Q\$ approximation (look here) and factor it with two cascaded poles. You end-up with a low-entropy expression, exactly what the FACTs will always naturally lead you to.

Answer 2

From the following schematic:

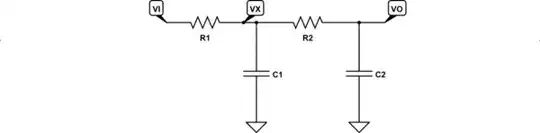
^{simulate this circuit – Schematic created using CircuitLab}

I get the following set of expressions using nodal analysis:

$$\begin{align*} \frac{V_\text{O}}{R_2} + s\: C_2\: V_\text{O} &= \frac{V_\text{X}}{R_2}\\\\ \frac{V_\text{X}}{R_1} + \frac{V_\text{X}}{R_2} + s\: C_1\:V_\text{X} &=\frac{V_\text{I}}{R_1} + \frac{V_\text{O}}{R_2} \end{align*}$$

Solving for \$V_\text{I}\$ and \$V_\text{O}\$ and dividing, I get:

$$\begin{align*} H\left(s\right)=\tfrac{V_\text{O}}{V_\text{I}}&=\frac{1}{R_1\,R_2\,C_1\,C_2\,s^2+\left(R_1\,C_1+R_1\,C_2+R_2\,C_2\right)s+1} \end{align*}$$

Since \$C=C_1=C_2\$ and \$R=R_1=R_2\$ this simplifies into:

$$\begin{align*} H\left(s\right)=\tfrac{V_\text{O}}{V_\text{I}}&=\frac{1}{R^2\,C^2\,s^2+3 R\,C\,s+1} \end{align*}$$

If you set \$\omega_{_0}=\frac{1}{R\,C}\$ then:

$$\begin{align*} H\left(s\right)=\tfrac{V_\text{O}}{V_\text{I}}&=\frac{\omega_{_0}^2}{s^2+3\,\omega_{_0}\,s+\omega_{_0}^2} \end{align*}$$

The standard low-pass 2-pole form (see equation (3) here for my reasoning of its development) is:

$$\begin{align*} H\left(s\right) &=\frac{\omega_{_0}^2}{s^2+2\,\zeta\,\omega_{_0}\,s+\omega_{_0}^2} \end{align*}$$

So it follows that \$\zeta=1.5\$ and that the system is over-damped (greater than 1.) Expected for a passive low-pass.

Answer 3

You are correct that you cannot do it in this manner because currents flow between your subnets. Instead of using two-pole analysis for the network, you can use four-pole analysis. Then you get

\$\begin{pmatrix}V_i\\I_i\end{pmatrix}=\begin{pmatrix}1&R_1\\0&1\end{pmatrix}\begin{pmatrix}1&0\\C_1\,s&1\end{pmatrix}\begin{pmatrix}1&R_2\\0&1\end{pmatrix}\begin{pmatrix}1&0\\C_2\,s&1\end{pmatrix}\begin{pmatrix}V_o\\I_o\end{pmatrix}\$

Setting \$I_o=0\$ gives you the relation between \$V_i\$ and \$V_o\$. One can easily recognize how the left-to-right circuit with series and parallel components translates into a left-to-right matrix product.

Inverting that relation gives you

\$\displaystyle\frac{V_o}{V_i}=\frac{1}{C_1 C_2 R_1 R_2 s^2 + (C_2 R_2 + C_2 R_1 + C_1 R_1)\, s + 1}\$

of course assuming an ideal voltage source at the input (so that voltage and current are independent on the left) and no current on the output.

With \$R_1=R_2=R\$, \$C_1=C_2=C\$ and \$RC=\tau\$, you get

\$\displaystyle \frac{V_o}{V_i}=\frac{1}{\tau^2s^2+3\tau s+1}\$