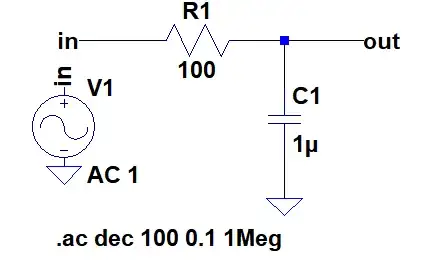
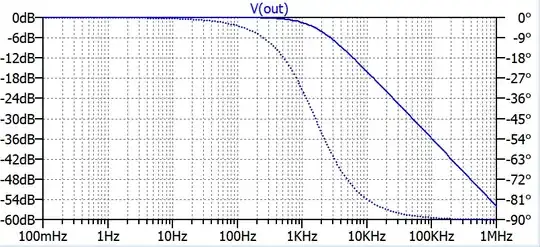
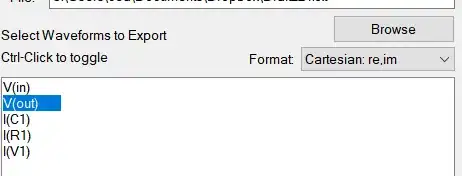
I'm trying to obtain transfer function given Bode plot data points. As an example I used the following RC filter and made AC sweep as follows:
I set the type of sweep to decade and for each decade the number of points as 100 points.
Then I exported the sweep to a txt file in Cartesian format as shown below:
Below is the first rows of Bode plot data saved to the text file from LTspice(first column is frequency the second column is the complex number):
1.00000000000000e-001 9.99999996052158e-001,-6.28318528237456e-005
1.02329299228075e-001 9.99999995866102e-001,-6.42953946745921e-005
1.04712854805090e-001 9.99999995671278e-001,-6.57930267936173e-005
1.07151930523761e-001 9.99999995467271e-001,-6.73255432451136e-005
1.09647819614319e-001 9.99999995253650e-001,-6.88937565895025e-005
1.12201845430196e-001 9.99999995029962e-001,-7.04984983141642e-005
1.14815362149688e-001 9.99999994795731e-001,-7.21406192743033e-005
1.17489755493953e-001 9.99999994550462e-001,-7.38209901440824e-005
1.20226443461741e-001 9.99999994293633e-001,-7.55405018782651e-005
Here is the Python code which reads and plots the exported LTspice Bode data.
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
dataset=pd.read_csv("Draft224.txt",delimiter=r'[\t,]', header=None, engine='python')
f = dataset[0]
re = dataset[1]
ima = dataset[2]
mag = np.sqrt(np.power(re,2)+np.power(ima,2))
plt.subplot(2, 1, 1)
plt.semilogx(f,20*np.log10(mag),'.r')
plt.semilogx(f,20*np.log10(mag),'-b')
plt.xlabel('Frequency [Hz]')
plt.ylabel('Magnitude [dB]')
plt.show()
plt.grid()
plt.subplot(2, 1, 2)
deg = np.rad2deg(np.arctan2(ima,re))
plt.semilogx(f,deg,'-g')
plt.xlabel('Frequency [Hz]')
plt.ylabel('Angle [°]')
plt.show()
plt.grid()
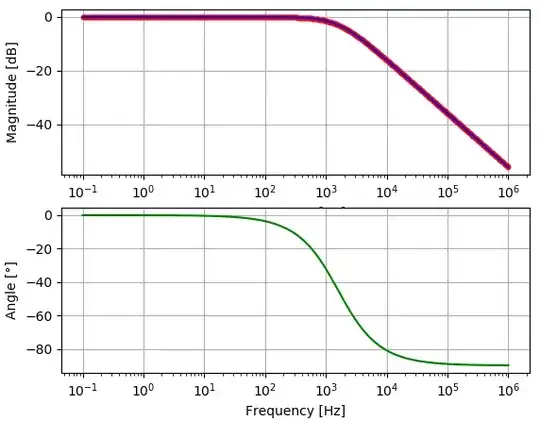
So this is the data plotted on Python which is the same shown in LTspice plot:
My question is:
Above I used LTspice as an example to create such data points. But such Bode plot data could be from a network analyzer or a data-acquisition system.
Having only the Bode plot data points of a system/circuit but not the circuit diagram, how can we obtain the transfer function?