-1

I am using scheme as shown below to blink an LED.

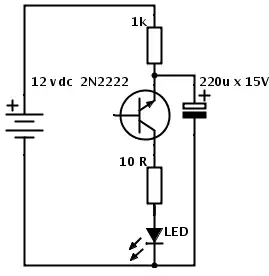
enter image description here

But I'm using 9V battery source instead of 12V.

I tried to use capacitors in range 100uF - 500uF to increase delay between blinks.

Questions:

  1. When I tried put there 1000uF capacitor, there is no more blinking effect. LED is OFF. Why?

  2. When I put there 500uF capacitor, I thought the LED will blink with 0.5s interval as 10K * 500uF should be Tau = 0.5s. Actualy I see it blinking with interval 0.25s.

JRE
  • 71,321
  • 10
  • 107
  • 188
naintrakusam
  • 21
  • 1
  • 2
  • 1
    Explain why you expect the circuit to blink a LED in the first place, with or without a capacitor present of any value you like. These is no mechanism present in this circuit to make the LED blink but please, prove me wrong, I might learn something. The only way this might work is if you use an "UJT" type transistor, like shown here: https://www.electroschematics.com/4852/mock-flasher-led/ But good luck finding an UJT as no one uses them anymore and they're probably not made anymore either. Simply use two transistors to make a LED blinker. – Bimpelrekkie Dec 23 '18 at 12:13
  • 1
    @Bimpelrekkie the base-emitter reverse breakdown voltage of many NPN transistors is ~6V. When that happens the transistor is reversed biased by its own breakdown current and it might act like an UJT due to the floating base node. – Edgar Brown Dec 23 '18 at 12:47
  • @Bimpelrekkie The emitter-collector "equivalent" diode act as a "tunnel diode" hence the negative-resistance region in the emitter-collector breakdown. https://electronics.stackexchange.com/questions/361846/is-it-possible-to-make-current-flow-through-a-transistor-from-the-emitter-to-the/361855#361855 – G36 Dec 23 '18 at 12:57
  • Esaki effect, OK, I buy that. Fact is, the reverse breakdown behavior with open base is very dependent on the actual transistor you're using. It works for some, it doesn't work for others. Like Edgar states "..and it might act like an UJT". So it might also decide not to work. I'd rather use 2 NPNs and have a reliable circuit. – Bimpelrekkie Dec 23 '18 at 14:16

1 Answers1

3

1. The original circuit is very fussy and this is why it will now always work. Because the BJT's does not work in his "typical" application. Also, your "big" cap can have too large leaking current. You could try to increase the supply voltage to 12V.

Also, this circuit is not recommended and it should be treated as an interesting circuit, but not as a reliable circuit.

2. The time constant equation will not work here. Because the capacitor is first charged via 1k resistor until the capacitor voltage reaches emitter-collector breakdown voltage. And this voltage will vary.

And then the capacitor will be quickly discharged via emitter-collector -- >10R resistor and LED. And in this case, your equation will not work.

The voltage across the capacitor will look something like this:

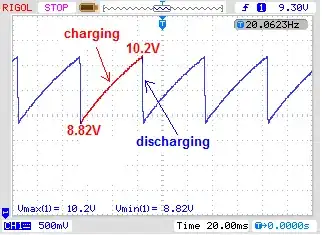
enter image description here

I use RED LED and Vcc = 12V and 2kΩ resistor, 47μF capacitr.

As you can see the voltage across the capacitor swings from \$V_{START}= 8.82V\$ to \$V_{END} = 10.2V\$ (when charging via 2kΩ resistor).

And to calculate how long it will take we need to use this equation:

$$T_1 = RC \cdot \ln\frac{V_{CC} - V_{START}}{V_{CC} - V_{END}}$$

And the discharge phase time

$$T_2 = RC \cdot \ln\frac{V_{END}}{V_{START}}$$

And in this circuit is hard to predict the discharging resistance value.

G36
  • 14,576
  • 1
  • 20
  • 36
  • Thx for explanation G36. Whats the reliable circuit then? Somebody here suggests circuit with 2 transistors – naintrakusam Dec 23 '18 at 17:52
  • @naintrakusam see here https://electronics.stackexchange.com/questions/336377/flashing-led-circuits/336388#336388 and this https://rayshobby.net/wordpress/learning-electronics-1-multivibrator/ – G36 Dec 23 '18 at 18:15