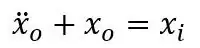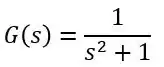Can the transient response of a system be calculated using FFT and inverse FFT?

Question

I have a system, its input and output has the following relationship.

I want to know the transient response of the system with respect to a ramping input Xi=t, by solving the differential equation, the response I obtained is

Xo= t-sin(t);

Now I want to obtain the transient response using another method,

i.e. first decompose the input signal into a series of sinusoidal signal

then calculate the system response of each sinusoidal signal

at last sum up all the responses of sinusoidal signal.

This method involves using FFT and inverse FFT. The detailed steps are

1. Calculate the transfer function of the system G(s). Substitute s=jw, this way I can get the complex number G(jw) with respect to each frequency w.

2. Process input signal using FFT to obtain the complex number with respect to each frequency component.

3. multiply the complex number in step 1 and 2 for the same frequencies.

4. using Inverse FFT to process the results obtained in step 3 to recover the signal in time domain.

I expected I could obtain the transient response using this method and the result should be same as the one I calculated by solving differential equation in time domain. But in reality, I was stuck at step 1. Because the transfer function of the system is

I found that at w=1 rad/s, this G(jw) is infinite. This means that if the input has a frequency component of 1 rad/s, going through the system (step 3), the amplitude of this frequency component will be amplified to infinite. Obviously this will lead to a transient output different from the one I got earlier.

Can anyone point out where I did wrong? If everything I did is correct, does that mean we can't obtain transient response by using this frequency analysis method?

Answer 1

First theoretical mistake to point out is trying to apply FFT (Fast Fourier Transform) to a continuous-time signal, since it would only make sense for discrete-time. If you actually mean just FT (Fourier Transform), then you'll be digging yourself into a hole, since the FT for a ramp is not very pretty: wikipedia link.

Instead, you should be thinking Laplace. The Laplace transform \$X(s)\$ for a ramp \$x(t) = t\$ is:

$$ X(s) = \frac{1}{s^2} $$

The Laplace transform \$Y(s)\$ of the output \$y(t)\$ will be:

$$ Y(s) = G(s)X(s) = \frac{1}{(s^2+1)s^2} $$

The Laplace inverse \$y(t)\$ can then be given by partial fractions:

$$ Y(s) = \frac{1}{s^2} - \frac{1}{s^2+1} $$

$$ y(t) = t-\sin(t) $$