How can capacitance values be determined from a cyclic voltammogram?

Question

I am reading an article (Khomenko, Electrochimica Acta 2005, 50, 2499-2506) that investigates the capacitance of carbon-based electrodes for use in supercapacitors. In particular, they use cyclic voltammetry (CV) to determine two types of electrodes (a PPy/MWNTs electrode, Figure 3, and a PANI/MWNTs electrode, Figure 4):

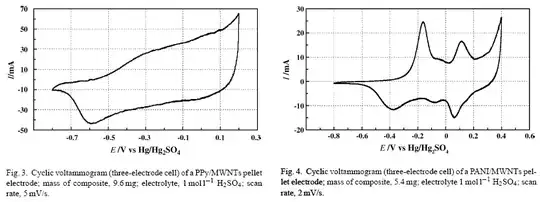
From these CV plots, the authors determine the capacitance values of each electrode:

The capacitance value was obtained from the CV curves according to the equation \$C = \frac{i}{s}\$ where \$i\$ is the average current and \$s\$ is the potential sweep rate. According to this formula, the cathodic charge determined by integration of the negative sweep of the CV curves is very high for such electrodes. The capacitance is \$670 \text{ F/g}\$ and \$506 \text{ F/g}\$ of electrode for the PANI and PPy composite electrodes, respectively.

I have a few questions about this method:

1. Why do the authors say that "the cathodic charge determined by integration of the negative sweep of the CV curves is very high"? Why do they refer to the cathodic charge, rather than the anodic charge?

2. What is meant by the average current \$i\$? What sort of average is meant? Do they mean consider a single sweep (either the part of the CV curve in which \$E\$ goes from negative to positive, or the part of the CV curve in which \$E\$ goes from positive to negative), and then integrate this sweep to find the average \$I\$? Recall from calculus that the average value of a function \$f(x)\$ in the interval \$a \leq x \leq b\$ is given by \$\bar{f} = \frac{1}{b-a} \int_a^b f(x) \; dx\$. Then does this mean that $$i = \frac{1}{\text{0.4 V } - \text{ -0.8 V}} \int_{\text{-0.8 V}}^{\text{0.4 V}} I(E) \; dE \;\;\;\;\text{ for the (-) to (+) voltage direction}$$ or $$i = \frac{1}{\text{ -0.8 V } - \text{ 0.4 V}} \int_{\text{0.4 V}}^{\text{-0.8 V}} I(E) \; dE \;\;\;\;\text{ for the (+) to (-) voltage direction}$$?

Answer 1

Under a given voltage the ideal capacitor obeys the following relationship:

\$Q = CV\$ where Q is the charge, V is the voltage applied and C is the capacitance. If we sweep the voltage with time then we can rewrite this as,

$$\frac{dQ}{dt} = C \frac{dV}{dt} $$

where \$dQ/dt\$ is the current and \$dV/dt\$ is the scan rate. It turns out that an ideal capacitor would be a rectangle during a CV scan. Unfortunately resistances present in the system lead to non-ideal behavior and cause rounding of the corners for our perfect square. The equation above is really just what the paper uses but with different symbols; upon rearrangement we see that we can get $$C = \frac{ \frac{dQ}{dt} }{ \frac{dV}{dt} } = \frac{I}{s} $$

So how do we use this technique to get our capacitance? Easy, we'll take the current starting from 0 current to either a maximum cathodic or anodic current going in one direction (in either a positive direction or a negative direction) and divide that by the sweep rate to get the capacitance of the device. In an ideal case it shouldn't matter which direction you pick, either the anodic or cathodic, but non-idealities may make one current give a higher capacitance. You can tell by looking on figure 3 that it is not perfectly symmetrical about the 0 current horizontal line, therefore the integrated area will be larger in one direction rather than the other.

For the second part of your question, recall that an ideal capacitor should give completely flat horizontal lines once charged, but in this experiment there is a slope, but for the equation used we depend on the capacitance being constant no matter the applied voltage once charged: so the authors have simply forced their data to fit to an equation for the ideal capacitor. They are probably just taking the average of the current for the voltage span of interest and then plugging it into the equation.