feedback resistor value for a crystal oscillator

Question

Does the feedback resistor for a crystal oscillator need to have a very accurate value? If a 16Mhz crystal requires 1Mohm, should one expect a problem when 200kohm or 2Mohm is used instead?

Answer 1

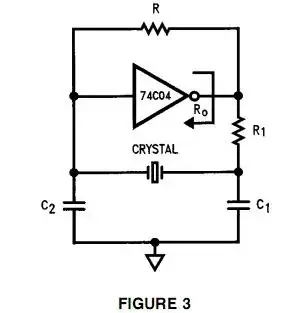
If you are using a standard crystal oscillator configuration like this: -

Then you have to be a little careful about lowering "R" because it can reduce the overall phase shift from output to input from reaching 180 degrees. The phase shift needs to reach 180 degrees in order to have a total phase shift around the loop of 360 degrees in order for the circuit to oscillate.

If you look at the diagram below I've simulated a pierce oscillator crystal circuit and used approximate equivalent values for the crystal for it to resonate at about 9.2 MHz (for convenience). I am particularly interested in the phase shift hence I'm doing an open loop AC simulation: -

With the feedback resistor at 1 Mohm (R3), the crystal and associated external components attains a phase shift of 180 degrees at 9.189 MHz. This is the oscillation frequency. As you can also see there is scope to reach a phase shift that is a few degrees more and so we would be assured that with typical component tolerances, the circuit would oscillate very close to 9.189 MHz.

If I now lowered R3 to 100 kohm I would be more uncertain of the oscillator working (due to component tolerances) because the phase angle exceeds 180 degrees to a lesser extent: -

So, the answer is "it depends" on what you equivalent circuit of your crystal is and what other external components are needed around that crystal such as R2, C3 and C4.