1

I am attempting to design a PR control feedback loop for a grid tie inverter. The math checks out but I can't seem to convert the transfer function and/or block diagram into an actual electrical circuit. Please find the block and transfer function attached. I would like to get an op amp circuit to implement this 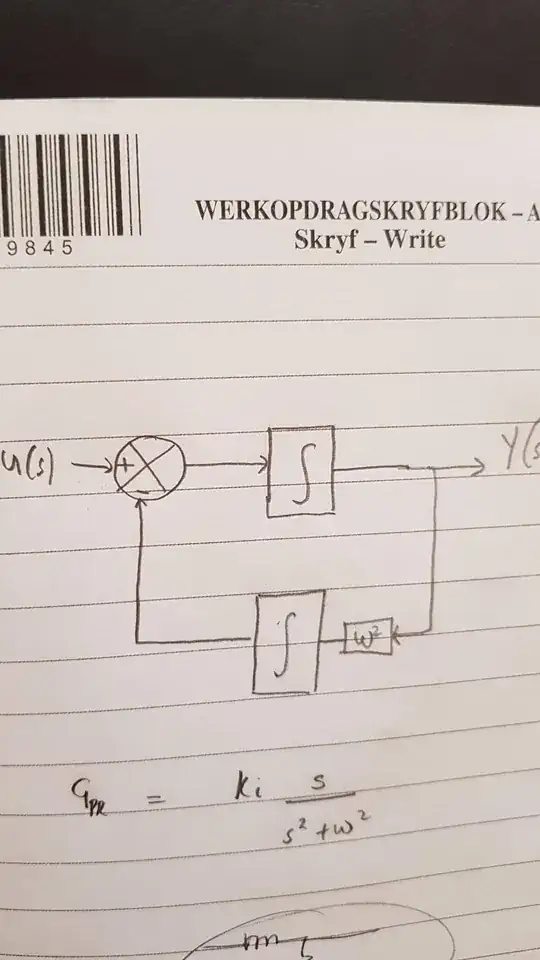block diagram

Ande Mandoyi
  • 11
  • 1

2 Answers2

2

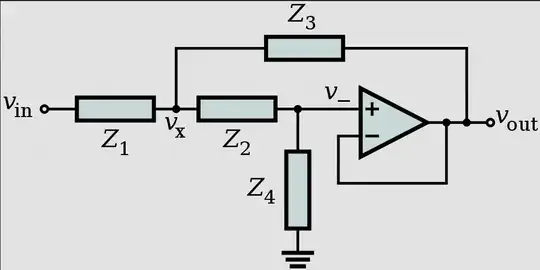
Normally you would find an op amp topology such as a sallen key:

enter image description here

which the transfer function would be

$$ H(s)=\frac{Z_3Z_4}{Z_1Z_2+Z_3(Z_1+Z_2)+Z_3Z_4}$$

And typically resistors \$ Z_x(s)=R\$ and capacitors \$ Z_x(s)=\frac{1}{Cs}\$ are used in these types of active filters.

There are also other realizable transfer functions that you can build with op amps:

enter image description here Source: slideplayer.com

However the transfer function you supplied is not realizable with general filters:

$$ H(s)=\frac{Ks}{s^2+w^2} \neq \frac{Z_3Z_4}{Z_1Z_2+Z_3(Z_1+Z_2)+Z_3Z_4}$$

because there is a middle term in the polynomial, no combination of high pass or low pass filters can used to construct your desired loop.

I will say this, an integrator is achieved this way with opamps:

enter image description here Source: electronics-tutorials.ws/opamp/opamp_6.html

$$ H(s)=\frac{1}{sRC}$$

So you could use that in your top and bottom portion of the loop.

If your looking to simply shift the frequency, then use a PLL, described here. Or a circuit such as an orthogonal signal generator

Voltage Spike
  • 82,181
  • 41
  • 84
  • 220
1

That looks like a Second Order Generalized Integrator (SOGI). In LTspice, it would look like this:

sogi

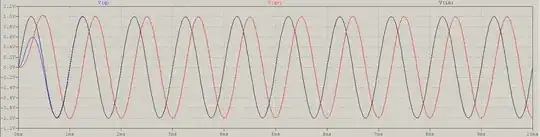
Time domain response:

time

Frequency response:

freq

G1, R1 form the error amplifier, G2, C1 the first integrator, and G3, C2 the second. These are, usually, implemented in a DSP, since the control is done digitally, and since you'd normally need several stages of these, one for each harmonic.

There are several version of a SOGI, this one is the simplest, yours looks like it allows for correction with external \$\omega t\$ signal, others have a stabilized loop, other corrections, etc.

a concerned citizen
  • 21,445
  • 1
  • 23
  • 40
  • 1
    That's a strange looking op-amp. – Harry Svensson Apr 19 '18 at 11:57
  • @HarrySvensson It's a behavioural model, since I've mentioned that, usually, they're implemented in DSP software. But, yes, that's an integrator, and nobody says an integrator must be with an opamp. – a concerned citizen Apr 19 '18 at 12:16
  • By the way, this could be done with a single bv-source. Or if you really need the signals, three bv-sources. – Voltage Spike Apr 19 '18 at 18:48
  • @laptop2d I know, but the whole point is getting the signals, because it outputs a quadrature (the outputs of each integrator). – a concerned citizen Apr 19 '18 at 19:32
  • @aconcernedcitizen Can you elaborete for a novice: What do these symbols (apparently not op-amps) represent? My best guess is like an op-amp but with a current output instead of voltage? – flawr Sep 28 '21 at 22:25
  • 1
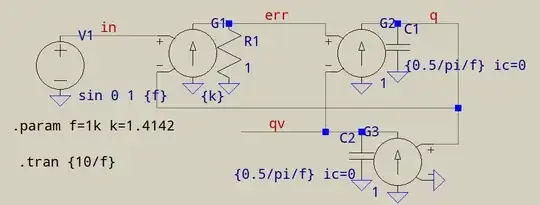
    @flawr The voltage across a capacitor is the integral of the current though it, and together with the VCCS acts as an integrator (input voltage converted to current, integrated by the capacitor, voltage output). G1 and R1 are the equivalent of a VCVS (voltage controlled voltage source), a simpe gain. – a concerned citizen Sep 29 '21 at 07:04
  • Thanks that makes sense! Are there any actual ICs that implement a voltage controlled current source? (So far I've only found circuits using op-amps to do this.) – flawr Sep 29 '21 at 08:01
  • 1
    @flawr A VCCS is nothing but a transconductance, so anything like the old LM13700 will do. Don't forget that the picture above is the ideal, behavioural schematic for a SOGI. As mentioned, in practice this is done in a DSP, because the quadrature is exact (within numerical limits), as opposed to an analog version which can have tolerances all over the place. – a concerned citizen Sep 29 '21 at 08:21
  • @VoltageSpike I have no idea how I missed your comment, but I did. With late regards, yes, it could have been done that way, but somehow I doubt the OP would have understood much of it. – a concerned citizen Jan 24 '22 at 11:22