Are the noise floor and signal to noise ratio same things?

Question

I have a problem in understanding clearly what noise floor is. The term SNR is more clear which is the ratio of the signal to the noise in dB.

In wiki the term noise floor is explained as:

In signal theory, the noise floor is the measure of the signal created from the sum of all the noise sources and unwanted signals within a measurement system, where noise is defined as any signal other than the one being monitored.

I still don't understand what it means mathematically or graphically. It says " measure of the signal created from the sum of all the noise sources and unwanted signals within a measurement system,.." I don't get what "measure of" means in this context.

How can noise floor be explained in a more clear way?

The whole sentence is blur. I still am not sure what noise floor is. Is it the power of the total noise in Watts? Some even below told me a sinusoidal noise cannot be noise ect. Not a clear idea what it means still. — user1245, Feb 17 '18 at 03:23
The noise floor is the sum of signals that is always there without the desired signal. The signal to noise ratio is the ratio between the desired signal and the noise floor. Think of an analogue AM radio where you did not tune into a station: the rain-like noise you hear is the noise floor. — rexkogitans, Feb 17 '18 at 10:39
Noise is any signals you don’t want. The noise floor is the sum of all signals in your system you don’t want. This means any signal you do want must be more powerful than the noise. — quamrana, Feb 17 '18 at 10:41

score 15 · Answer 1 · answered Feb 16 '18 at 20:48

15

A helpful way to think of the two concepts is suppose your final measured signal is a superposition of two functions:

$$ f = f_s + f_n $$ where \$f_s\$ is your signal, and \$f_n\$ is the noise.

The signal to noise ratio would be a measure the relative power of these two signals:

$$ SNR = \frac{P(f_s)}{P(f_n)} $$

Note that the SNR doesn't tell you anything about the "absolute" power of the noise; it is only a relative measure of how much stronger your desired signal is vs. the noise. You can have a lot of noise, but as long as your desired signal is much stronger you can still have a good SNR (think of someone using a megaphone in a really large crowd).

The noise floor is just a measure of the noise itself; that is, you can think of it as \$P(f_n)\$; how much noise do you have, regardless of whatever signal there is. This is like asking the question "how loud is the crowd I'm in?", and doesn't depend on any signal at all.

answered Feb 16 '18 at 20:48

helloworld922

16,770
10
56
88

1

Can you give an example for noise floor as you did for SNR. So the noise floor is the voltage peak to peak value of the noise? Lets say 1mV pk-pk sinusoidal noise is superimposed on a 1V DC signal. What is the noise floor here? – user1245 Feb 16 '18 at 21:31
1

@user134429 sinusoidal noise If it's a sinusoidal signal, it would be predictable and that means it would not be noise. We usually define noise in an RMS value so not peak and also in a certain bandwidth. Noise doesn't have a peak value as you don't know when the peak (voltage) is reached, you might have to wait forever! RMS is more convenient, then we can relate the noise to power as dissipated in a resistor. That also means it is an averaged value. A DC voltage doesn't carry any information so it does not influence the noise. Yep, noise isn't so easy ;-) – Bimpelrekkie Feb 16 '18 at 22:14
@user134429. One could say the ratio between a 1 volt RMS signal and a 1 mV RMS signal is 60 dB, or a 1,000:1 ratio. – Feb 16 '18 at 22:19
Why is it too complicated to define what noise floor is? Why dont you just say it is the power of the total noise in Watts? Isnt that? – user1245 Feb 17 '18 at 05:39

score 2 · Answer 2 · answered Feb 16 '18 at 20:44

2

The SNR is a ratio between a signal and noise. The "noise floor" is exactly that reference level of noise that determines the SNR.

answered Feb 16 '18 at 20:44

Ale..chenski

40,470
3
39
109

score 2 · Answer 3 · answered Feb 17 '18 at 04:45

2

The noise floor is the amount of noise you have in your system. You get SNR by dividing the amount of signal you have by the amount of noise you have. It's typically measured in either units of power (Watts) or power in a given frequency (Watts/Hz).

Noise floor is a convenient concept because it's tied to your receiver's hardware rather than the signal's strength. Take a radio as an example. It can't control the signal's strength. That's controlled by the radio station and the distance between the station and the radio. If I wanted to talk about the specs on the radio using SNR terms, I might have to say "The system needs a SNR of -18dB when receiving a signal from a 100kW radio station 1km away with an antenna whose gain is 0.7." That's a lot of numbers. If I phrase it in terms of a noise floor, I might be able to say "The system needs a noise floor of 15uW." You could, of course, convert one to the other (don't try -- I totally made the numbers up), because they are asking for the same kind of thing. Just one of them is specified in terms of the noise on its own, while the other has to factor in the signal.

answered Feb 17 '18 at 04:45

Cort Ammon

2,916
13
19

Why is it too complicated to define what noise floor is? Why dont you just say it is the power of the total noise in Watts? Isnt that? – user1245 Feb 17 '18 at 05:36
1

@user134429 I did define noise floor. That was my first sentence. The reason I don't just say it's the power of the noise in Watts is because that's not the only way the concept is used. It's a statistical concept which is adapted to whatever makes the most sense at the time. For example, if I was designing a DSL system to connect someone's house to the internet, I can choose how much bandwidth my system operates on. I can trivially decrease the power of the noise by using a smaller band. – Cort Ammon Feb 17 '18 at 15:10
So, for purposes of designing that system, it may make the most sense to define my noise floor in terms of the bandwidth. I may say I have 3uW/kHz of noise, meaning every 1kHz band has 3uW of noise. Or I might even have something like 1mW/octave, which would indicate that between any two frequencies F and 2*F, there's 1mW. Whatever the most useful measure is, that's what we'd use. – Cort Ammon Feb 17 '18 at 15:11
However, you choose to measure it and quantify it, the noise floor is the concept of how much noise you have in the system. – Cort Ammon Feb 17 '18 at 15:12

score 1 · Answer 4 · answered Feb 17 '18 at 03:34

In a digital channel, sinusoids within the passband that degrade the Bit Error Rate should be modeled as noise.

Yes, there is no average-to-crest energy, but the BER tells all.

BER plots will sometimes include a combination of random and deterministic trash. Jitter at various frequencies needs to included in these BER models.

In cell site and cell subscriber models, the adjacent channel energy (overloading the IF amplifiers) and the same-channel energy (degrading the constellation, by scattering the points) must be included in Channel BER thinking.

score 1 · Answer 5 · answered Feb 17 '18 at 13:57

Are the noise floor and signal to noise ratio same things?

No. Signal to Noise Ratio (SNR) is the relative strength of the signal to the noise. It's a comparison.

Noise Floor is the absolute measurement of noise.

I still don't understand what it means mathematically or graphically.

When you look at a model or system and you want to measure something, in an ideal world there is no noise. In the real world other signals that you don't want to measure are always present and interfering with the signal you do want to measure.

Noise is simply any signal you are uninterested in. It usually comes from the environment that you're measuring, but it can come from many sources, including your measurement system itself.

So, mathematically, you might have signals S₀ through S₃, but you're only interested in measuring S₁.

The SNR is S₁ / (S₀ + S₂ + S₃) - the ratio of the signal you want to measure over the signals you don't want to measure - the noise.

The noise floor is S₀ + S₂ + S₃ - the absolute value of the signals you don't want to measure.

Here is a graphical example. The top four graphs on each side are the four signals, the bottom graph is the sum of each side's signals. On the left you'll find the magnitude of the second graph, S₁, is low compared to the magnitude of the noise sources S₀, S₂, S₃. It's hard to find much evidence of that signal in the bottom graph, which is what you're measuring trying to find S₁. The right side shows a stronger signal and weaker noise sources, and it's easier to visually pick out the desired signal.

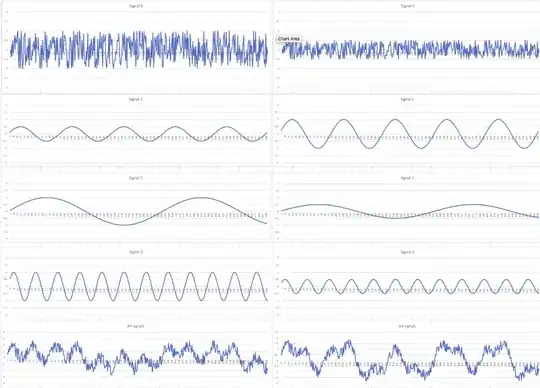
However, it's hard to discern a noise floor from a graph. Under certain circumstances, such as when the signal is strong and has distinct features (such as a square wave) then people will point to the ever-present noise centered around the x axis, with the signal clearly popping above that noise, as the "noise floor" - but this is something to be calculated and measured, and not derived graphically, so it's not helpful to show such images and use them to define noise floor because you'll eventually be presented with such an image, perhaps from a oscilloscope screen, and unless you can subtract the intended signal from the noise it will not always be obvious what the noise is.

Graphing, in general, is a poor way to explain this anyway, because the graph on the left, though it appears difficult to pick out S₁, can actually result in a good reading of the presence or absence of S₁, and if that's all you're looking for then the SNR and noise floor are fine. If S₁ is a more complicated signal, carrying more data per cycle, etc, then the SNR and noise floor presented might be sufficient to prevent you from recovering the data.

the noise floor is the measure of the signal created from the sum of all the noise sources and unwanted signals within a measurement system, where noise is defined as any signal other than the one being monitored.

I don't get what "measure of" means in this context.

It references the later phrase, "measurement system" so it's defined by the method you are using to measure the system.

Most commonly you'll find people using decibels (dB), but you'll also find, depending on the measurement system, that the units are Watts, bits, voltage, current, and many other units and methods of measuring. Switch to the frequency domain and you'll get different units there as well.

There is no specific standard for the units, and thus noise floor is unit-less as defined, and when you use it you must always specify the units.

SNR is a ratio, and doesn't require units, but typically units are given so you can use that number to derive the signal or noise magnitude if you know the other, as well as giving some hints as to what measurement system was in use.

Are the noise floor and signal to noise ratio same things?

5 Answers5