BiCMOS Amplifier with feedback for DC bias and AC

Question

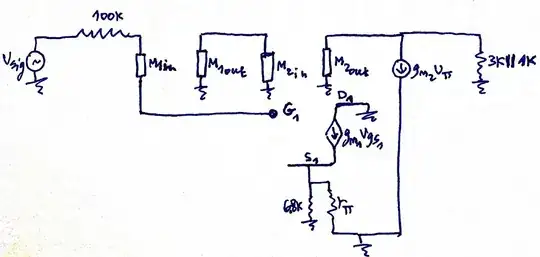
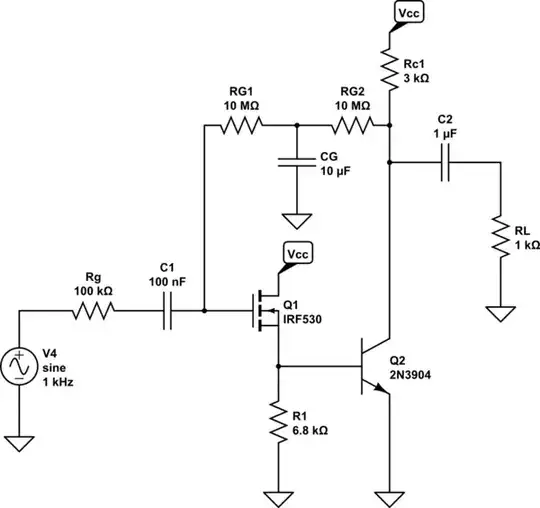
In the following circuit, to considerably reduce the effect of RG on Rin and hence on amplifier performance, another 10MΩ resistor was added in series with the existing one and a large bypass capacitor between their joint node and ground was placed. What will Rin, AM, and fH become?

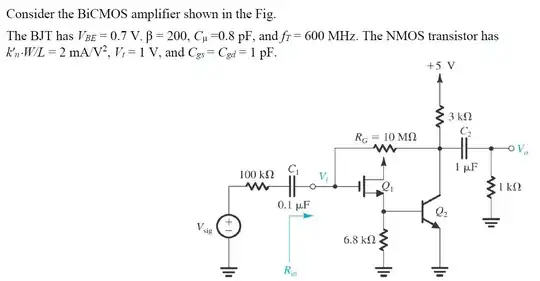
Here's my attempt:

\$V_i-V_x+V_o-V_x=10M\cdot V_x/(j\omega C)\$

I know \$V_o/V_i\$ of the original circuit, in midband frequency, which shouldn't change in this case. Let's denote that \$x\$.

I can hence infer that:

\$K_1=V_x/V_{in}=(1+x)/(2+10M/j\omega C)\$

and

\$K_2=V_o/V_x=(2+10M/j\omega C)\cdot x/(1+x)\$

Therefore,

\$M1_{in}=10M/(1-K_1)\$

and

\$M1_{out}=10M \cdot K_1/(K_1-1)\$

Similarly,

\$M2_{in}=10M/(1-K_2)\$

and

\$M2_{out}=10M \cdot K_2/(K_2-1)\$

Is this the right way to solve this? Is there a simpler approach? I figured now I could easily determine \$R_{in},f_H\$, as requested.

Why don't you use a sim? It's a basic circuit and a sim should perform really well. — Andy aka, Jun 10 '17 at 09:36
How to solve this: 1) find the DC solutions for Q1 and Q2 because you need to know their gm. 2) draw the small signal equivalent circuit of Q1, Q2 and find the gain from Vi to Vo. 3) now that you know Vo/V1 solve with 100 k Rsource and Rg in place. — Bimpelrekkie, Jun 10 '17 at 10:05
@Bimpelrekkie I already did that but now I need to assess how the new configuration would affect my results. In my attempt I tried to elaborate how to account for the changes. Does my work make sense to you? — peripatein, Jun 10 '17 at 10:18
No, I do not see how you can have a 2nd 10 Mohm resistor in there. Study how to solve amplifiers with feedback and apply that. — Bimpelrekkie, Jun 10 '17 at 10:24
@Bimpelrekkie The question stated explicitly "another 10MΩ resistor was added in series with the existing one and a large bypass capacitor between their joint node and ground was placed" — peripatein, Jun 10 '17 at 10:26
You don't ever need to know Vx, at DC you just solve the circuit as Rg= 2*10Meg, at AC Vx is grounded. — sstobbe, Jun 10 '17 at 12:00
@sstobbe so in AC the value of RG would simply be 5M and I could use Rin=5M/1-K, where K=midband voltage gain? — peripatein, Jun 10 '17 at 12:05
Bypass cap means short circuit at signals of interest. So you have a 10Meg resistor to ground on the input and a 10Meg resistor to ground on the output. No resistor connects the output to input, since the bypass cap shorts to ground. — sstobbe, Jun 10 '17 at 12:09
@sstobbe why couldn't they be evaluated in parallel, hence my 5M? — peripatein, Jun 10 '17 at 12:12
Its because the only have one terminal connected together, at the bypass cap. The other terminal of the resistor is connected to different parts of the circuit. — sstobbe, Jun 10 '17 at 12:15
@sstobbe Okay, so is my new Rin=10M, new fH=1/(2pi(10M+100k)), new AM=old AM (as I was told that in determining the small signal voltage gain I could ignore RG)? — peripatein, Jun 10 '17 at 12:17
@sstobbe Right, silly me, what I meant to write was rather fH=1/(2pi(100k+Min)), where Min=5M/1-K and where K=AM, midband voltage gain. Is that correct now? — peripatein, Jun 10 '17 at 12:32
Millers theorem only applies to Cu on Q2. So fH will either be due to Cgd on Q1 on M*Cu on Q2 — sstobbe, Jun 10 '17 at 12:38
@sstobbe Here's another attempt -- fH=1/(2piCgd*(Min+100k)). Is it correct now? — peripatein, Jun 10 '17 at 13:12
@sstobbe Let's see if I understand: before RG was changed, fH was 1/(2piCgd(Min||100Kohm)), where Min=10M/1-K and K is midband voltage gain. This yielded fH=2.075MHz. After another 10M was added in series with a bypass cap. fH changed to 1/(2piCgd10Meg||100K), yielding fH=1.607MHz? — peripatein, Jun 10 '17 at 13:28
Sounds reasonable, also note the gain is slightly different for the two cases, as Rsig divides into Min — sstobbe, Jun 10 '17 at 13:52

score 1 · Answer 1 · answered Jun 10 '17 at 09:51

1

Is there a simpler approach?

My simple approach is that with the original circuit you have negative feedback at all frequencies therefore the input impedance at the gate is close to zero ohms. That's how negative feedback works. It's a virtual earth as per an op-amp virtual earth.

With the modified feedback (and C being a large capacitor as stated) there is only negative feedback at DC and very low frequencies hence, at significantly higher frequencies, there is no feedback hence the input impedance is 10 Mohm (the left resistor in your added/modified circuit).

That's about as simple an approach as you can get.

answered Jun 10 '17 at 09:51

Andy aka

456,226
28
367
807

My approach above yielded Rin=0.7M for a very large C. Is my approach therefore wrong? Where exactly is it incorrect? – peripatein Jun 10 '17 at 10:20
I think you need to show the precise circuit you assumed. I could be misinterpreting what you say you did in the second scenario. – Andy aka Jun 10 '17 at 10:35
Well, I simply did: Rin=M1_in || M2_in whilst substituting C-> inf. – peripatein Jun 10 '17 at 10:37
No, draw a circuit. – Andy aka Jun 10 '17 at 10:37
I added my circuit under my main attempt above. What do you think? – peripatein Jun 10 '17 at 10:46
A proper circuit that shows how the second network fits in with the original circuit. – Andy aka Jun 10 '17 at 11:29
how about now? Better? – peripatein Jun 10 '17 at 11:47
No, not better, I can't make head nor tail of that. Show it as a proper circuit and not as your interpretation. I want to see transistors drawn as transistors and not as small signal models that might be subject to your misinterpretation. – Andy aka Jun 10 '17 at 12:16

G36 · Answer 2 · 2017-06-10T15:36:23.267

0

The circuit looks like this:

schematic

^{simulate this circuit – Schematic created using CircuitLab}

DC operation point is \$I_{D1} \approx \frac{0.7V}{6.8kΩ} \approx 100 \mu A \$

And \$V_{GS1} = V_T+\sqrt{\frac{I_D}{0.5K'n}}\approx 1.3V\$ and \$ I_{C1} \approx \frac{5V - (0.7V + 1.3V)}{3kΩ} \approx 1mA \$

And for AC signal

schematic

^{simulate this circuit}

And from inspection we can see that \$ R_{in} = R_{G1} = 10MΩ\$

And the AC voltage gain is:

$$ A_V = -\frac{R_{G1}}{R_g + R_{G1}} *\frac{R1||((\beta+1)*r_e)}{R1||((\beta+1)*r_e) + \frac{1}{g_{m1}}}*\frac{R_{C1}||R_L||R_{G2}}{r_e}*\frac{\beta}{\beta+1} \approx -18.8$$

edited Jun 10 '17 at 15:36

answered Jun 10 '17 at 15:29

G36

14,576
1
20
36

And the MOSFET gm1 is ? – G36 Jun 10 '17 at 15:49
You're right, except that I got approx. -19.1, instead of approx. -18.8. By the way, if I wished to find fL of this circuit, hence to determine the frequency of the poles due to C1 and C2, could I use OCTC to obtain this: fL=1/(2pi[C1(100K+3K+10M)+C2(4K)])? Would that be correct? – peripatein Jun 10 '17 at 16:00
But for FL we suppose to use Short-Circuit Time Constants – G36 Jun 10 '17 at 16:05
AS for FL we have FL1 ≈ 0.16/((Rg+RG1)C1) ≈ 0.16Hz and FL2 ≈ 0.16/((Rc+RL)C2) ≈ 40Hz hence FL ≈ 40Hz – G36 Jun 10 '17 at 16:23
And for FH we have two poles Fh1 ≈ 0.16/( (Rg||RG1) Cgd+ Cgs(1 - A1) ) ≈ 0.16/(100k * 1pF+1pF(1 - 0.666)) ≈ 0.16/(100k1.4pF) ≈ 1.14MHz. Where A1 is Q1 gain. – G36 Jun 10 '17 at 16:53
Fh2 ≈ 0.16/(R1||rpi||1/gm1 * Cbe + Cbc(1+A2)) ≈ 0.16/(1k 10pF + 0.8pF30) ≈ 0.16/(1k34pF) ≈ 4.7MHz where A2 is Q2 gain – G36 Jun 10 '17 at 16:55
What's Cbe? It's not given in the question – peripatein Jun 10 '17 at 18:09
Not directly, but if we know Ft and gm we can find Cbe = gm/(2pi*Ft) - Cbc – G36 Jun 10 '17 at 18:27
Do I find the total fH by 1/[sum(time constants)] or do I use the square root formula? – peripatein Jun 10 '17 at 19:37

BiCMOS Amplifier with feedback for DC bias and AC

2 Answers2