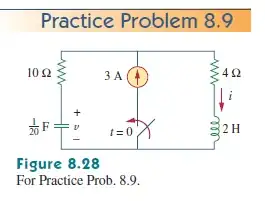
Your initial conditions are correct. There is no short circuit in here. Take a look at the circuit. We have 2 time intervals:
@t<0:
- the switch is open. without a return path back to its source, there
can be no current
- You essentially have a circuit with NO sources; the current source is
an open circuit
@t--> infinity:
circuit is in steady state:
this means the capacitor is open and the inductor is shorted into a
wire
By definition, a wire has no potential difference.
Since there is an open, the resistor behind the capacitor receives no
current, and has zero volts (ohm's law).
- The capacitor itself is fully charged to maximum voltage, but is not
considered in kvl analysis because it is open.
- In essence, you have a single Kvl loop with inductor, current source and
resistor. ==> I=3, VL=0, Vr=4*3=12v.
- Since the resistor is in parallel with the capacitor, they share the same
voltage: 12v.
From here, you can set up the second order equations need to solve for the transient responses, so I'll leave it to you.
Hint: decide what type of RLC circuit it is, whether it's critically, under, or overdamped, and go from there.