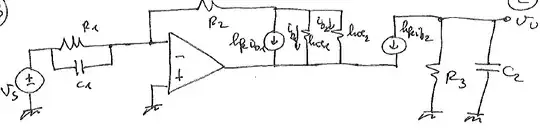
When I study frequency responce of amplifiers, I must understand if capacitors are in serie, parallel etc. relative to input small signal (in my exercises there is always only one input small signal). So far I learned that:
a capacitor in parallel to the input small signal introduces an infinite zero and a finite pole;
a capacitor in serie to the input small signal introduces a finite zero (equal or not equal to 0) and a finite pole;
a capacitor in other configuration introduces a finite zero and an infinite pole? Is this third point right?
For example, if I consider the following circuit:
the capacitor C2 is in parallel to the input small signal, in fact for w=infinity the vu=0. Is the capacitor C1 not in serie or parallel (for w=infinity --> vu is not 0; for w=0 the vu is not 0)?
Thank you in advance.