1

I have the following magnetic circuit problem:

Core

For the left hand core, the mean path length calculated in the solution manual is 1.11m. However what I don't understand is, why is the length of the air gap included? Don't you have to subtract the air gap length from the total length of the core?

SamGibson
  • 17,870
  • 5
  • 40
  • 59
hacker804
  • 602
  • 5
  • 19
  • I don't see why you would subtract the length of the air gap: the magnetic field flows through it as well. – DavideM Oct 08 '16 at 07:48
  • @DavideM Because the iron core and the air gap have a different reluctance. – hacker804 Oct 08 '16 at 07:58
  • 2
    With or without the gap, the answer is the same within 1mm or better than 1 part in 1000. Now consider the "mean path length" is a convenient fiction - a pretty crude approximation to the path that will actually be taken by the flux - you'll see some concentration around the inner edges for example. Errors in that approximation will swamp the error in length introduced by the gap, so the simpler approximation will be good enough. –  Oct 08 '16 at 09:43
  • Yes you are right the answers are more or less the same if I include that minuscule length or not.

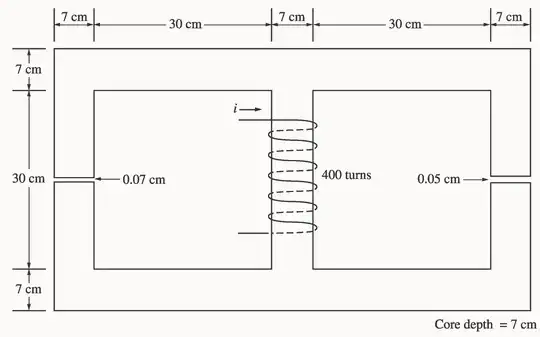
    Thanks

     – hacker804 Oct 08 '16 at 09:53
  • The actual path length that you calculate by geometry will not be correct, in practice. – Chu Oct 08 '16 at 10:48

1 Answers1

2

Let's say you hand made a core from finely ground iron powder and used some kind of epoxy to bond those particles into the correct shaped core.

What you have is a core that will be good for many tens of kHz working because the individual grains of powder are insulated. This prevents induced eddy currents in the core due to the vast majority of grains not contacting each other.

This is sometimes also referred to as a distributed air gap and behaves pretty much like a physical air gap but, would you have a problem with calculating the mean length of the magnetic field now?

Andy aka
  • 456,226
  • 28
  • 367
  • 807