-2

How do I calculate the radius of a copper wire dissipating heat of 100mW given that the volume of the conductor is 20mm^3 and is carrying a current of 40nA. Resistivity of copper is 0.0000172.

Null
  • 7,603
  • 17
  • 36
  • 48
Mark.Wambua
  • 15
  • 2
    You have current and power, calculate resistance. You then have resistance and resistivity, calculate cross-sectional area. You then have area, calculate radius. – Ignacio Vazquez-Abrams Oct 01 '16 at 09:34
  • must be a really long nano-filament I^2R=P, R=0.1/16e-20 – Tony Stewart EE75 Oct 01 '16 at 10:18
  • Do you REALLY mean nA = nano amps. That's 40 x 1/1,000,000,000 A OR 40 x 1/1000,000 mA or 40 x 1/1000 microamp. I suspect that you MAY mean 40 mA. – Russell McMahon Oct 01 '16 at 10:28
  • 4
    I'm voting to close this question as off-topic because it looks like homework. – Leon Heller Oct 01 '16 at 10:51
  • 1
    Units and the number of zeros after the decimal point are both kinda important in engineering. Your resistivity number appears to have more than one problem. It is certainly not in SI units, even if the Cu was molten. – Spehro Pefhany Oct 01 '16 at 11:38
  • @IgnacioVazquez-Abrams. It's not quite that easy. – EM Fields Oct 01 '16 at 15:53
  • @LeonHeller: So it looks likes homework. So what? Isn't it an interesting, multifaceted problem which should be addressed respectfully instead of being dumped on the trash heap of your vanity? – EM Fields Oct 03 '16 at 19:00

1 Answers1

1

  1. Get the reference resistance from your question:

    $$R=\frac{P}{I^2}= \frac{0.1W}{40\cdot10^{-9}A^2} = 6.25\cdot10^{13} \text{ ohms} $$

  2. Start out with a 20 cubic millimeter right circular cylinder of copper and set its radius to 1mm.

  3. Get the cylinder's length:

    $$ l =\frac{V}{\pi\ r^2} =\frac{ 20mm3}{3.14 \times1mm2} = 6.369 \text { mm} $$

  4. Get the cylinder's cross-sectional area:

    $$ A = \pi\ r^2 = 3.14\times1^2 = 3.14\text { mm2}$$

  5. Get the cylinder's resistance along its length:

    $$R=\frac{\rho\ l}{A} = \frac{1.72 \cdot10^{-5} \Omega\ mm \times 6.369mm}{3.14mm2} $$

  6. Compare the resistance of the cylinder with that of the reference and if the resistance of the cylinder is >= that of the reference, stop.

  7. If it's < that of the reference, squeeze the cylinder to elongate it.

  8. Go to 3.

It'll take about 1 049 303 iterations and, at the end, the wire's cross-sectional radius will be about \$ 2.74\cdot10^{-9}\text { millimeters}\$

Just for fun, here's a link to the source code for a tiny PowerBasic program I wrote to do the grunt work,

https://www.dropbox.com/s/a0qfpmu2ukafxu2/Long%20wire%203.bas?dl=0

The executable:

https://www.dropbox.com/s/p11jl6yot0bhems/Long%20wire%203.exe?dl=0

and the output screen just in case you don't want to run the .exe

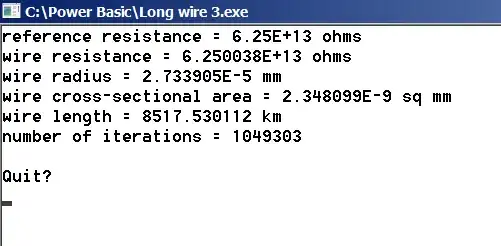
enter image description here

Nick Alexeev
  • 38,181
  • 17
  • 100
  • 237
EM Fields
  • 17,527
  • 2
  • 19
  • 23
  • Oops... 1. is wrong. I'll fix it presently – EM Fields Oct 02 '16 at 16:39
  • Thank you very much for the interest you have shown in helping me tackle this problem. Am waiting for the fix. – Mark.Wambua Oct 02 '16 at 17:07
  • @Mark.Wambua: My pleasure. It's an interesting problem and I think I fixed my solution. – EM Fields Oct 02 '16 at 17:56
  • There's still a problem in explaining the solution , but I can't get to it just now... Perhaps tomorrow. – EM Fields Oct 02 '16 at 18:52
  • So a wire diameter of 5.48 x 10e-12 meters, which is impossible because the diameter of a single Copper atom is 2.28 x 10e-10 meters - 42 times larger that the 'wire'! – Bruce Abbott Oct 02 '16 at 23:56
  • I got stuck too @EMFields. I will really appreciate. – Mark.Wambua Oct 03 '16 at 07:10
  • @BruceAbbott: Unless I made a mistake somewhere along the line, you've shown that the problem was nonsensical. – EM Fields Oct 03 '16 at 10:42
  • Always verify the results you get. Plug the radius back into the formula's, and confirm you really get 100mW. I think the result should be: r=154nm (l=270km). – peter Oct 03 '16 at 10:51
  • @peter: I think you may have missed the point, which was that for a 20 cubic millimeter volume of copper configured as a wire with a uniform cross-sectional area, there's only one area and length which will satisfy the dictates of the specified current through, and power dissipated by, the wire. – EM Fields Oct 03 '16 at 18:10
  • You got the right answer, but you sure took the long way around. Given that volume $V = length\cdot area$ and resistance $R = \sigma\frac{length}{area}$ (where $\sigma$ is resistivity), it's easy to combine them to get $length=\sqrt{\frac{R\cdot V}{\sigma}}$. This gives the same solution you have, and once you have the length, it's easy to get the area and then the radius from that. – Dave Tweed Oct 03 '16 at 21:45
  • @EM Fields: Anyone can verify for themselves that a cylinder with r=154nm and l=270km has a volume of 20 cubed mm.
    %pi(15410^-9)^2 * 27010^3; gives me 2.010-8     – peter Oct 03 '16 at 23:03