3

I understand how CDMA works (kind of). I'm just not sure how to go about figuring out how many orthogonal signals can be produced from a code length of a given number.

user922467
  • 33
  • 2
  • 1
    There's some really, really hairy math to get that number. I took a grad course in wireless and we didn't cover that formula. Have you tried Google Scholar? This is definitely something that would have ended up in a publication. – Mike DeSimone Nov 30 '11 at 02:27
  • I haven't tried it. I read the book we have and went over the lecture notes. This is an entry level networking class for my undergrad degree. I'm feeling a little overwhelmed by this question. – user922467 Nov 30 '11 at 03:12
  • @MikeDeSimone I am not sure what the hairy math that you are talking about would be. The only thing I can think of is when you start to look more at power usage, noise, etc. – Kellenjb Nov 30 '11 at 13:58
  • The hairy math was in identifying the needed code patterns. Your example is simple, but it looks like TDMA, and I thought that you could get more users than code bits if you were willing to trade off some interference. (Noise isn't nearly as much of an issue in cell phone systems as interference, so they usually speak of an S/I ratio.) In other words, I see your solution as a lower bound, but I'm not sure it has to be an upper bound. – Mike DeSimone Dec 01 '11 at 03:58
  • @MikeDeSimone The OP specifically asked about orthogonal signals which is what I answered to. This is not TDMA at all as the orthogonal domain that I am talking about is the code domain, not the time domain. If you increase your codes beyond what I have described, you will be almost guaranteed to have bit errors when all of your users are talking concurrently, which is also what he asked about. – Kellenjb Dec 01 '11 at 14:53
  • The professor is looking for completely orthogonal signals. To me that means that they wouldn't produce any noise between each other. So I need to know the maximum of such orthogonal signals given a code length of n. By brute force I tried all combinations of code lengths 2 and 4 on paper and came up with 2 and 4 orthogonal signals that could be made, respectively. This obviously has no mathematical basis to conclude that the answer is n, but I am willing to accept it as my answer and move on to my next homework question. – user922467 Dec 01 '11 at 15:22
  • @user922467 If you have taken a linear algebra course of any sort, there are proofs to show how many orthogonal vectors you can fit into any given domain, but you probably don't want to go through those proofs. – Kellenjb Dec 02 '11 at 16:08

1 Answers1

3

Note: I am going to go into a bit of the algebra that goes into understanding CDMA fully. It might be a little overwhelming at first, but I will try to keep it as simple as I can. If you just want the answer, jump to the bottom, but it really isn't as difficult as you might think. Also, I am an engineer, not a mathematician, and many of the things engineers do with math drive mathematician crazy. I may simplify things to the point that the math gets a little fuzzy, but it is all for the sake of understanding.

In order to fully understand how many concurrent senders you can have, you need to step back and make sure you understand what it means to be orthogonal. The simplest way to look at orthogonality is to visualize it in a 2-d or 3-d plane. 2 vectors are orthogonal when they are at 90* angles of each other. So for a 2d plane you get something like this:

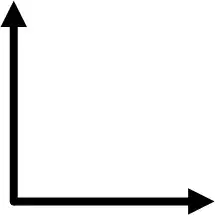
enter image description here

These two vectors might be represented as something like [01] and [10].

As it works out, there is no way for you to add a 3rd vector to those existing 2 vectors and and have it also be at a 90* angle to both existing vectors. It is possible to add a line that would be at a 90* angle to one of the existing lines, but not both, you should be able to see that visually. This can also be called a basis set, but that isn't overly important unless you want to dive deeper.

This then can also be extended visually into a length 3 vector space which shown graphically is like this:

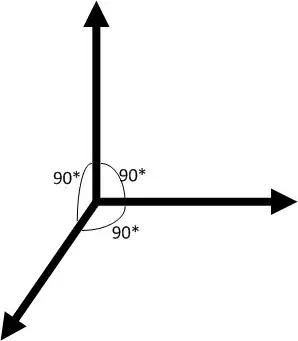
enter image description here

where the line to the bottom left is actually coming out at you in a 3d model. As you can see we were able to add 1 more vector that is at 90* to both of the existing two vectors. We were unable to do this until we extended the length of our vector to 3. These 3 vectors could be represented as [100] [010] and [001].

So as you hopefully can see from my above examples, you are able to have N vectors that are orthogonal to each other when the vectors are of length N. In other words. Length 2 means you can get 2 orthogonal vectors out of it, length 3 means you can get 3 orthogonal vectors out of it.

Now, how does that apply to CDMA and number of users? Well each CDMA channel is created by an orthogonal code, so you can support as many concurrent users as you have orthogonal codes, and you can have as many orthogonal codes as you have length of the code. (if you need more help understanding this part I will be willing to add more, just let me know)

So to summarize, a length N code results in being able to support N number of concurrent users.

Kellenjb
  • 17,609
  • 5
  • 53
  • 87