Reactive Power in Inductor and Capacitor

Question

Suppose a RLC circuit with AC source. Why the net reactive power in the circuit is the difference of reactive power in the inductor and the reactive power in the capacitor ? As both of them store power then why the reactive power in them is not added instead of subtraction.

Answer 1

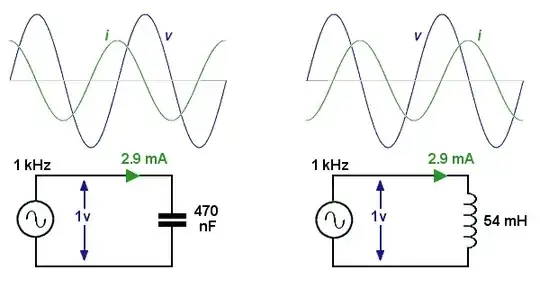
Current leads voltage in a capacitor. Voltage leads current in an inductor. I was taught this using the CIVIL spelling:

In a C I leads V leads I in an L. (I hope that makes sense.)

The effect is that the voltage or current will be 180° out of phase between the inductor and the capacitor and so in summing them they tend to cancel out rather than add.

As both of them store power then why the reactive power in them is not added instead of subtraction.

Both of them store energy but one will be maximum while the other is minimum. This effect is seen best in the resonant circuits where the energy flows back and forth between the inductive and capacitive elements.

Answer 2

As both of them store power then why the reactive power in them is not added instead of subtraction.

Both of them store energy not power. Power is the rate at which energy is stored or transferred. Anyway, moving on...

For a capacitor Q = CV and if you differentiate Q you get: -

\$\dfrac{dQ}{dt} = C\dfrac{dV}{dt}\$ and, of course rate of change of Q is current therefore you can say: -

\$I = C\dfrac{dV}{dt}\$. This means if the applied voltage (V) is a sinewave then the current is a cosine wave: -

Now if you looked at an inductor you would find that \$V = L\dfrac{dI}{dt}\$.

If you integrated both sides to find I then you would see that \$I = \dfrac{\int{V}\cdot dt}{L}\$.

Clearly if V is a sinewave then I must be a negative cosine wave. Here are the two scenarios side by side: -

So, if you have an L and a C in parallel across a sinewave voltage source, then the current in the inductor is exactly opposite in polarity to the current in the capacitor i.e. while one is taking energy from V, the other is delivering energy back to V. This gives rise to the currents being subtracted.

It's also notable that when the impedances are identical (one specific frequency) as indicated on the diagram immediately above, the net current into a parallel LC is zero i.e. they behave together as an infinite impedance. This is called parallel resonance and is extensively used in radio. It's also called power factor correction in electrical engineering; you find a value of capacitance that keeps the PF unity thus keeping the reactive energy "consumed" to a minimum.