3

My textbooks usually just assert this relation so I don't really know when it doesn't apply.

EDIT: Reflecting on this question, I wanted to clarify that I wanted to know if Ohm's Law is valid for the analysis of time-varying current/time varying voltage/ time varying load i.e., V(t) = I(t)R(t).

Minh Tran
  • 307
  • 1
  • 3
  • 13
  • 5
    Time to learn about impedance and phasors. – Ignacio Vazquez-Abrams Jan 09 '16 at 07:44
  • @Ignacio what about disputers? :p – Passerby Jan 09 '16 at 08:10
  • 1
    It stil applies. However, it is much more rare to encounter a pure Resistance in AC. Often there are other reactive impedances. – Mark Ch Jan 09 '16 at 09:12
  • Capacitors, inductors act different in AC than in DC in inear circuit. – user16307 Jan 09 '16 at 09:34
  • @Ignacio Vazquez-Abrams What does knowing about impedance and phasors have to do with knowing if V=IR applies in AC circuits? Isn't impedance just a time-varying "resistance" expressed as a ratio of time-varying Voltage divided by time-varying Current? – Minh Tran Jan 09 '16 at 19:27
  • @MinhTran: Yes. But they're out of phase if you have any reactance. – Ignacio Vazquez-Abrams Jan 09 '16 at 19:30
  • @MinTran: I am not an expert but a resistor causes resistance. Resistance not only limits the current according to ohm's law I=V/R, but also uses up energy, or removes energy from the system in form of heat. Impedance consists of resistance and reactance, but it is only the pure resistance part of the impedance that uses up energy, the reactance part can be said to store energy. – fredrik.hjarner Jan 09 '16 at 21:24

5 Answers5

5

\$V=IR\$ is always valid in any circuit at any frequency but there are some things to watch out for and be aware of when the frequencies get really high or when there are non-linearities such as diodes to consider.

In an AC circuit V= IR like this: -

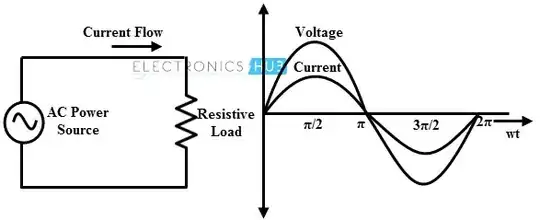
enter image description here

In other words I and V follow each other and have a constant ratio to each other. That constant ratio (V/I) is still R. For other types of components like capacitors the relationship between V and I is more complex: -

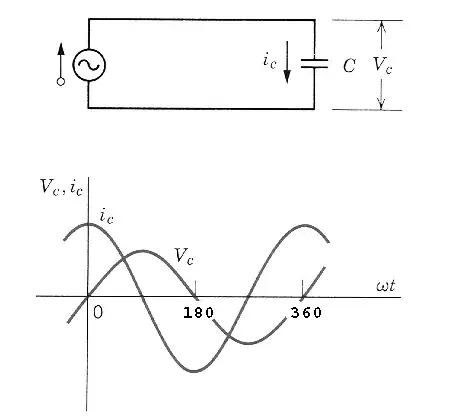
enter image description here

Now the current is "time displaced" and does not rise and fall in sync with the voltage.

Given that any resistor has a small amount of parasitic capacitance means that at high frequencies there begins a subtle change in the phase relationship between V and I. This change gets bigger and bigger at really high frequencies and, the resistor begins to look more like a capacitor.

I've purposely not mentioned inductors just to keep the answer simple.

Andy aka
  • 456,226
  • 28
  • 367
  • 807
2

Simple answer: Yes, Ohm's Law still applies in AC circuits.

The difference is that AC circuits involve complex sources and impedances which vary with either time or frequency, so your \$V, I, \&\ R\$ aren't always real numbers, but complex expressions. Nevertheless, the relationships established in Ohms Law for DC circuits will ALWAYS apply.

0

Yes, generally you can, but you should also take into account electromotive force produced by C and L in your circuit at each time point.

kelin
  • 151
  • 1
  • 4
  • 1
    This doesn't sound quite right. See electromotive force: 'Electromotive force, also called emf (measured in volt), is the voltage developed by any source of electrical energy such as a battery or dynamo.' – Transistor Jan 09 '16 at 12:02
  • Well, may be I've selected wrong term. In russian physics school we call Electromotive Force everything that can create potential difference, including capacitor charge, or magnetic field change in the inductor. – kelin Jan 09 '16 at 12:07
0

It is used in DC analysis mostly. For AC analysis, you will need to learn impedances too.

Miss P
  • 19
  • 1
  • 4
  • 1
    For inductors, $V = L\frac{\partial I}{\partial t}$, and for capacitors, $V = \text{initial value} + \frac{1}{C}\int_t I(t) \partial t$. This turns the analysis of AC circuits from an algebra problem into a calculus problem (differential equations). – Dave Tweed Jan 09 '16 at 15:14
0

Of course, the Ohms's Law is still valid in AC circuits too. However, you will have to look out for components like capacitors, inductors (commonly used in AC Circuits) which have a different behavior relative to resistors. The mathematics dealing with them, is different as it climbs up into Complex Domains.

Vatsal Garg
  • 1
  • 1