1

simple circuit

  1. How does the voltage/electric field of the battery relate to the surface charges on the wire?
  2. What determines the amount of surface charge on the wire? (Why more near the battery, less farther away)
  3. What are the surface charge doing?
m0meni
  • 143
  • 5
  • I'm not the "-1", but just as an effort to explain, your questions makes no sense (or at least are physically inaccurate). It would help if you could cite your source for these claims and/or explain what you think "surface charges" are... – DrFriedParts Mar 26 '15 at 06:22
  • Related: https://electronics.stackexchange.com/questions/532541/is-the-electric-field-in-a-wire-constant/532550#532550 – Sredni Vashtar Nov 08 '21 at 03:37
  • @DrFriedParts perfectly conventional physics, and it looks suspiciously like a homework problem directly from a physics textbook. (The conductor is clearly a resistor here, so assume nichrome wire, carbon ribbon, etc.) For much info, see Chabay/Sherwood college textbook "Matter and Interactions," the EM electric circuits chapter in volume 2. – wbeaty Nov 08 '21 at 05:46
  • @wbeaty -- Obviously, with enough assumptions it can be made to fit. The fact it's poorly clarified in the question, and that you're likely correct that it's a copy-paste homework problem, explains why the (likely) student posted the question in the first place. – DrFriedParts Nov 11 '21 at 12:25

3 Answers3

2

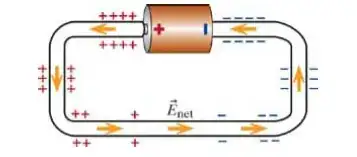
You may find this document helpful, since it seems to be the primary source for the popularization of this idea. The short version is that the battery creates an electric field which pushes on the electrons in the wire. The field looks vaguely like this:

Electric dipole field

According to the above source, calculating surface charge distribution is extremely difficult. But if you look at the direction of the field lines and imagine your wire imposed on top of it, you can see that the electric field is going to be pulling electrons away from the left side and pushing them towards the right side. The surface charges eventually distribute themselves so as to create a uniform electric field throughout the wire:

Ultimately, this elegant negative feedback mechanism will produce an arbitrarily complex distribution of surface charge all over the wire such that the electric field due to all the charges (surface charge plus the charge on the [voltage source]) is uniform throughout the wire and has the magnitude predicted by conservation of energy (the Kirchhoff loop rule).

Adam Haun
  • 21,959
  • 4
  • 51
  • 91
1

In conventional terminology "surface charge" describes the voltage (potential difference) between the opposing sides of a bi-state boundary (ex. liquid-gas, liquid-solid, etc). In your example you have only solids and therefore no "surface charge" by that convention.

By the most trivial interpretation, surface charges are everywhere in the metal wire and since the battery is the only electric field generator in the scenario, the field is constant and therefore the mobile charges on the surface of the wire are uniform (ideal, infinite wire). They don't cluster near the battery, nor reduce further from it.

In practical (and practical scale systems) you can perturb the distribution of charges in the wires, but it's irrelevant unless you are considering near-field effects. Since perturbations will cancel in the far-field to create the constant electric field required by the static sole-source configuration.

You may be misinterpreting the question asked of you, as it may refer to the surface charge induced on another object placed near the wire loop rather than on the wire in the picture itself.

DrFriedParts
  • 12,562
  • 37
  • 54
  • Note that the wire in his diagram must be a resistor, rather than an ideal short circuit. Physics teachers see nothing wrong with (mentally) hooking copper wire across battery terminals, then calculate the voltage gradiant with the milli-ohm resistance and kilo-ampere currents. (An engineering teacher would just use nichrome wire here, or extremely thin tungsten, or perhaps a hose full of weak brine.) The whole diagram is about resistance, without any zero-ohm connecting wires to make things more complicated. – wbeaty Nov 08 '21 at 05:52
  • @wbeaty -- I guess, but it's incredibly sloppy on the part of the authors, both in their use of terminology and their application. They're mixing ideal and applied terms and forcing a lot of assumptions on the part of the reader. Hard to see how that helps students grasp the underlying physics (more like, a "because I said so; go memorize"). – DrFriedParts Nov 11 '21 at 12:13
0
  1. The voltage is proportional to the surface charge density. A high density of negative charge corresponds to a high negative voltage. A low density of positive charge corresponds to a low positive voltage.

This is because a concentration of charge causes an increase in the electric potential energy (with sign equal to the sign of the charge, or opposite, depending on your convention) in those charges (lots of repulsion). A low density causes low repulsion and low potential energy.

Ultimately, you can consider voltage and charge density as roughly equivalent concepts, one is the direct consequence of the other.

  1. The distribution of charge is the result of a complex interaction between all elements in the circuit. But ultimately, what happens if that charge is accumulated at resistors, since there they lose velocity, more arrive than they leave. This in turn repels incoming charges, extending the accumulation all the way back to the voltage source.

On the other side of the resistor, there is a charge defect (since charge is conserved). In other words, an accumulation of the opposite charge.

In your case, there is no resistor, so the whole wire will act a a resistor. The effect I described then occurs in every point in the wire. Charges accumulate at the end of the battery, and de-accumulate towards the other extreme, as they get slower and slower because of the friction of the wire.

  1. The charges create electric fields, which drive the whole circuit. At each point in this wire, there is a stronger charge on one side than on the other, so there is a net field pushing the charges of one sign forward, and of the other, backwards.

In summary; The electric field from the battery pushed the charges, push the charges next to them, etc. Then the friction of the wire slows them down, causing accumulation of charges, which in turn causes more electric fields to push the charges. Eventually, a steady state is reached.

Juan Perez
  • 153
  • 1
  • 8