2

I have a servo motor with a torque of 10kgcm. My question is how much weight can it carry? I really don't understand "kgcm." Is there a way to calculate how much weight can a motor carry?

Devgeet Patel
  • 103
  • 2
drew
  • 21
  • 1
  • 1
  • 3
  • 1
    That motor can oppose a 10kg weight at 1cm from the rotor. or 1kg at 1m from the rotor –  Dec 22 '14 at 09:38
  • your question must be in physiqus. If we suppose T= Fr; with F is force and r is deplacent and F=ma; if we suppose that your speed is constant, than we have T=Mg with M is masse and g gravity. for Tmax you have Mmax=T/g. torque is measured in N*m and not in Kg/cm! – R Djorane Dec 22 '14 at 09:51
  • Use of kg.cm is "wrong" but common. Close enough 1 kg mass "weighs" 10 Newton (9.8 is closer still). A very naughty but useful approximation that is accurate within about 1% but works for the wrong reasons (but works!) is | Power = kilogram.metres x RPM | = kg.cm x RPM / 100 | ~~= N.m x RPM / 10 | ~= N.cm x RPM / 10 – Russell McMahon Dec 22 '14 at 12:10

3 Answers3

5

The rating is magnitude of the torque, which is simply the scalar magnitude of the vector cross product between force vector F and the lever arm displacement vector r. The units are force * distance (coincidentally the same as the units of work) and usually datasheets use mass units rather than force, so the force a certain mass experiences under 1G gravity.

http://upload.wikimedia.org/wikipedia/commons/0/09/Torque_animation.gif

In the case where the force is perpendicular to the lever arm and to the axis of rotation you can simply multiply the scalars. In other cases, the force will be transferred through the bearing or whatever is constraining the motion to be rotation about the axis.

In the example from Wikipedia shown above, if we visualize the earths gravity as being in the z axis, the weight the motor can drive is essentially unlimited if the rotation axis is vertical. That's because the motor need only provide the torque to accelerate the mass, and that can take place slowly for bigger masses.

If the rotational axis is horizontal with the lever arm perpendicular, then the maximum torque is when the lever arm is horizontal, and the magnitude is the length of the lever arm (say 1cm) multiplied by the force (that experienced by 1kg or about 9.8N).

The same torque can be created by 100g at 10cm or 10g at 1m.

If an equal lever-arm-times-mass was horizontally opposed (statically balanced) then there would be no hard limit to the mass, just as in the first case (at some point the friction in the bearings would cause problems).

It's like tightening or loosening a nut with a socket as shown on this page: enter image description here

The torque experienced by the nut is the cross product between the force applied to the ratchet handle and the lever arm. A longer lever arm means more torque for the same force.

Spehro Pefhany
  • 397,265
  • 22
  • 337
  • 893
3

That unit is incorrect. It should read "10kg⋅cm" (it should also be in terms of force, not mass, but we'll let that slide for a moment). That is to say, the product of the distance from the pivot point times the mass of the object to move (under Earth gravity) can be no more than 10.

So you could have a 2kg (under Earth gravity) mass 5cm away from the pivot point, or a 100g (under Earth gravity) mass 100cm away, and so on. Any more mass-distance and the motor will either be unable to turn or will be forced downwards.

Torque is usually measured in force-distance (in newton-meters, N⋅m), not mass-distance.

Ignacio Vazquez-Abrams
  • 48,488
  • 4
  • 73
  • 103
  • I think you're wrong, if we have T=10 Nm than we have 10N force for 1m distance if we suppose for the distance of 5cm than we have F=200N with F=mg for g=10 m/s^2 we have m=20kg. – R Djorane Dec 22 '14 at 10:12
  • 2
    @codo: OP has stated the torque in kg.cm, not N.m (as it is usually given, since it's SI). 1kg.cm is really 1kg-force.cm, which means the OP's torque figure is approx. 100N.cm or 1N.m. He's right, except that at 50cm away the equivalent mass is 200g, not 100g. – Mister Mystère Dec 22 '14 at 18:41
2

It will be 10kg if you put load 1cm from your servo axis.

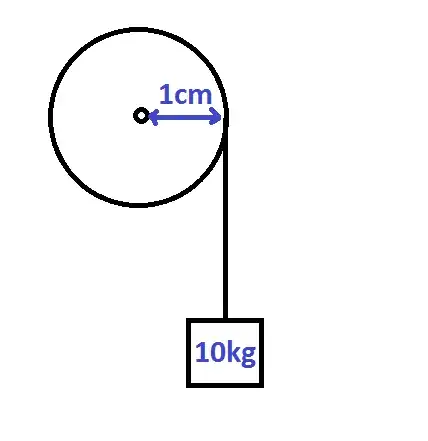
enter image description here

If you put it at 10cm from axis - it will be able to pull 10 times less (1kg). You can use Law of lever to calculate this.

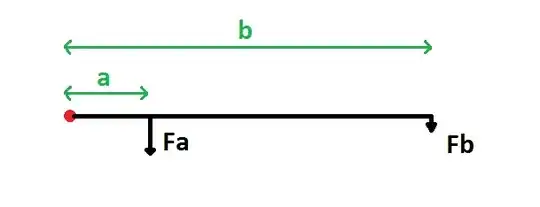
enter image description here

$$ \frac{F_{b}}{F_{a}} = \frac{a}{b}\ $$

If you need this for vertical lift - you can replace force with of mass.

Kamil
  • 6,004
  • 9
  • 43
  • 60