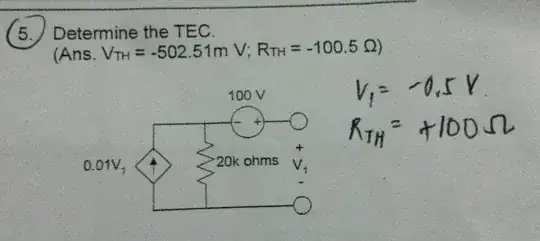
\$V_1\$: Your KCL equation is right, but it looks like you either rounded too much or misunderstood something. \$V_A\$ is not -100V, it's -100.50251V. You can get this via nodal analysis:
$$0.01*V_1 = \frac{V_A}{20k}$$
$$V_1 = V_A + 100$$
Thus:
$$0.01(V_A + 100) = \frac{V_A}{20k}$$
$$0.01*V_A + 1 = 0.00005*V_A$$
$$0.00995*V_A = -1$$
$$V_A = -100.50251V$$
$$V_1 = V_A + 100V = -502.51mV$$
\$I_{SC}\$: There's no need to do mesh analysis here. When you short the terminals together, two things happen. First, \$V_1\$ becomes 0V, so there's no current through the dependent source. Second, \$V_A\$ is fixed to -100V, which completely determines the resistor current. You got the right magnitude, but there's a sign error. Your short-circuit current is positive, since it comes from the positive end of the voltage source. It's just Ohm's Law:
$$\frac{V_1}{20k} = 5mA$$
You can get the resistance from there.
(The \$I_{SC}\$ calculation above has a very interesting implication -- when an ideal voltage source and a current source are in parallel, the current source has no effect at all! This is because an ideal voltage source will absorb or add to the current source's current in order to maintain its voltage. In the same way, when an ideal current source is in series with a voltage source, the voltage source has no effect. The current source can produce whatever voltage it needs to maintain its current.)