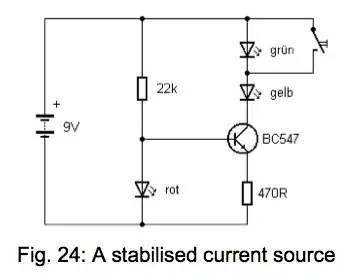
How does the red (rot) LED at the input to the base provide a constant current to the other two LED's after the collector, via the transistor? (I have been told that the NPN transistor here has a default voltage of 0.6v, and the red LED at the base is providing an additional 1.2v, for a total of 1.8v)
If I short-circuit one of the LED's, the brightness of the green (grun) and the yellow (gelb) LED does not fluctuate. What is happening when I do this?
The \$V_{BE}\$ of the transistor is about 0.6V, as you said. The rot LED has a \$V_F\$ of about 1.8V, so the voltage across the 470R resistor is about 1.2V. We can ignore the base current, since the BC547 typically has an \$h_{FE}\$ of several hundred. So, the collector current (which equals the LED current) is very close to 1.2V/470R = 2.55mA, regardless of the collector voltage (and therefore the LED drop of the gelb and grun LEDs).
Note that this only remains true while the transistor is out of saturation, so the collector voltage of the BC547 must be more than about 1.3V, so the LED string connected to the collector cannot drop more than 9V-1.3V = 7.7V.
How does the red (rot) LED at the input to the base provide a constant current to the other two LED's after the collector, via the transistor?
It doesn't - the LED provides an effectively constant voltage at the base of the transistor.
$$V_B = V_{LED} $$
The voltage at the emitter of the transistor is proportional to the current through the transistor:
$$V_E = I_E \cdot 470 \Omega$$
and the current through the transistor is related to the voltage across the base and emitter \$V_{BE} = V_B - V_E\$:
$$I_E \approx I_C = I_S e^{\frac{V_{BE}}{V_T}}$$
Now, there are two important observations:
(1) \$V_E\$ increases if the transistor current \$I_E\$ increases
(2) \$V_{BE}\$ and thus \$I_E\$ decreases if \$V_E\$ increases
In other words, if for any reason the transistor current increases, the base-emitter voltage decreases which acts to decrease the transistor current.
This is hallmark of negative feedback and, in this case, the negative feedback acts to keep the transistor current constant*.
If I short-circuit one of the LED's, the brightness of the green (grun) and the yellow (gelb) LED does not fluctuate. What is happening when I do this?
If you were to place an ammeter in series with the collector of the transistor, you would discover that there is an insignificant increase in transistor current (due to the Early effect) when you short-circuit one of the LEDs.
Recall from the previous section, negative feedback acts to keep the transistor current effectively constant so short-circuiting one of the LEDs does not significantly change the remaining LED's current and thus, the brightness does not change.
*This analysis does not take into account the Early effect but, for this circuit, the effect is insignificant.
If I short-circuit one of the LED's, the brightness of the green (grun) and the yellow (gelb) LED does not fluctuate. What is happening when I do this?
It's a constant current circuit (nearly) so shorting one of the LEDs out doesn't change the current (much) thru the other LED. This means its brightness stays about the same.
With 1.8V on the base, the emitter is about 0.6 volts lower at 1.2V and this means the current through the 470 ohm has to be about 2.6mA irrespective of what mainly happens at the collector.
While the other answers are correct, I'd like to add that the final result when you short one of the LEDs is that the voltage from the collector to the emitter of the BJT will compensate for the missing LED voltage-wise. So if one of the LEDs was taking up 1.8 volts, when you short it, the 1.8 volts will now be added to the BJT's collector-emitter voltage drop. The BJT now consumes that extra power that the LED previously did.
For even better performance you can use Two silicon diodes or another NPN instead and put the rot (Red) LED in the collector for RGB optional color combinations. Thus the current will be just one diode drop /Re for Re=33 Ohms I= 0.7/33 = 21 mA (typical rating =20mA nom.)
The 3 LEDs for R,G, B may add up to around 1.6 + 3.2 + 3.4 = 8.2 leaving just enough for the transistor.
Beta or hFE and LED ESR tolerance will add considerable variation so brightness may dim as 9V battery dies out. Deep Red has a lower Voltage than high efficiency Red.
Put 10% of the LED current into the Vbe for effective saturation and enough for the diodes to saturate, requires >2mA or Rb~450 Ohms or slightly less.