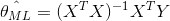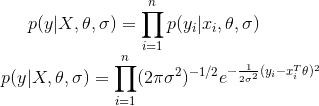Understanding the math behind using maximum likelihood for linear regression

Question

I understand both terms, linear regression and maximum likelihood, but, when it comes to the math, I am totally lost. So I am reading this article The Principle of Maximum Likelihood (by Suriyadeepan Ramamoorthy). It is really well written, but, as mentioned in the previous sentence, I don't get the math.

The joint probability distribution of $y,\theta, \sigma$ is given by (assuming $y$ is normally distributed):

This equivalent to maximizing the log likelihood:

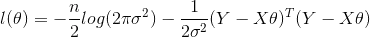
The maxima can be then equating through the derivative of l(θ) to zero:

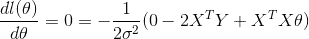
I get everything until this point, but don't understand how this function is equivalent to the previous one :

Answer 1

Note first that the first $=$ (equals) in $\frac{dl(\theta)}{d\theta} = 0 = −\frac{1}{2\sigma^2}(0−2X^TY + X^TX \theta)$ should be interpreted as a "is set to", that is, we set $\frac{dl(\theta)}{d\theta} = 0$. Given that (apparently) $\frac{dl(\theta)}{d\theta} = −\frac{1}{2\sigma^2}(0−2X^TY + X^TX \theta)$, $\frac{dl(\theta)}{d\theta} = 0$ is equivalent to $0 = −\frac{1}{2\sigma^2}(0−2X^TY + X^TX \theta)$.

Now, let's apply some basic linear algebra:

\begin{align} 0 &= −\frac{1}{2\sigma^2}(0−2X^TY + X^TX \theta) \iff \\ 0 &= −(0−2X^TY + X^TX \theta) \iff \\ 0 &= −0 + 2X^TY - X^TX \theta) \iff \\ 0 &= 2X^TY - X^TX \theta \iff \\ X^TX \theta &= 2X^TY \iff \\ (X^TX)^{-1}(X^TX) \theta &= (X^TX)^{-1}2X^TY \iff \\ \theta &= (X^TX)^{-1}2X^TY \end{align}

Now, you can ignore the $2$, because it is just a constant, and, when optimizing, this does not influence the result.

Note that using $\hat{\theta}$ instead of $\theta$ is just to indicate that what we will get is an "estimate" of the real $\theta$, because of round off errors during the computations, etc.