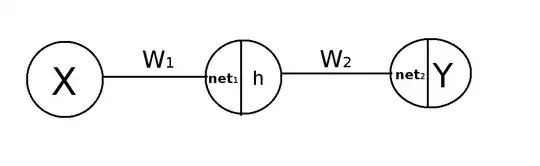
I have computed the forward and backward passes of the following simple neural network, with one input, hidden, and output neurons.
Here are my computations of the forward pass.
\begin{align} net_1 &= xw_{1}+b \\ h &= \sigma (net_1) \\ net_2 &= hw_{2}+b \\ {y}' &= \sigma (net_2), \end{align}
where $\sigma = \frac{1}{1 + e^{-x}}$ (sigmoid) and $ L=\frac{1}{2}\sum(y-{y}')^{2} $
Here are my computations of backpropagation.
\begin{align} \frac{\partial L}{\partial w_{2}} &=\frac{\partial net_2}{\partial w_2}\frac{\partial {y}' }{\partial net_2}\frac{\partial L }{\partial {y}'} \\ \frac{\partial L}{\partial w_{1}} &= \frac{\partial net_1}{\partial w_{1}} \frac{\partial h}{\partial net_1}\frac{\partial net_2}{\partial h}\frac{\partial {y}' }{\partial net_2}\frac{\partial L }{\partial {y}'} \end{align} where \begin{align} \frac{\partial L }{\partial {y}'} & =\frac{\partial (\frac{1}{2}\sum(y-{y}')^{2})}{\partial {y}'}=({y}'-y) \\ \frac{\partial {y}' }{\partial net_2} &={y}'(1-{y}')\\ \frac{\partial net_2}{\partial w_2} &= \frac{\partial(hw_{2}+b) }{\partial w_2}=h \\ \frac{\partial net_2}{\partial h} &=\frac{\partial (hw_{2}+b) }{\partial h}=w_2 \\ \frac{\partial h}{\partial net_1} & =h(1-h) \\ \frac{\partial net_1}{\partial w_{1}} &= \frac{\partial(xw_{1}+b) }{\partial w_1}=x \end{align}
The gradients can be written as
\begin{align} \frac{\partial L }{\partial w_2 } &=h\times {y}'(1-{y}')\times ({y}'-y) \\ \frac{\partial L}{\partial w_{1}} &=x\times h(1-h)\times w_2 \times {y}'(1-{y}')\times ({y}'-y) \end{align}
The weight update is
\begin{align} w_{i}^{t+1} \leftarrow w_{i}^{t}-\alpha \frac{\partial L}{\partial w_{i}} \end{align}
Are my computations correct?