curse of dimensionality v.s. volume of n-dimensional ball v.s. n-dimensional vector embedding space

Question

We know that the performance of machine learning model become worse if we feed the model with a few features and many features (high dimensional data). This is known as the curse of dimensionality.

The relationship between performance and the num of features/dimensions based on the most Google search is similar as follow, where the idea is finding the fit number of dimension in order to achieve the best performance:

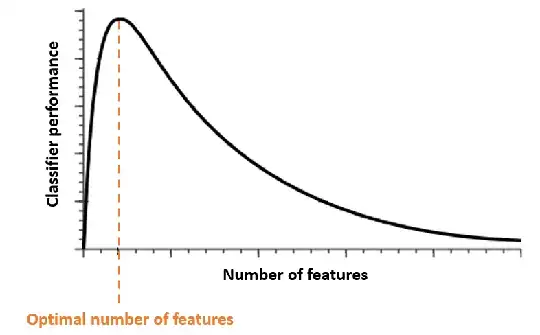
On the other hand, the graphic looks similar with the volume over n-dimensional ball. Where the x-axis represents n-dimension of ball and y-axis represents volume (for n=2, it's called area of circle):

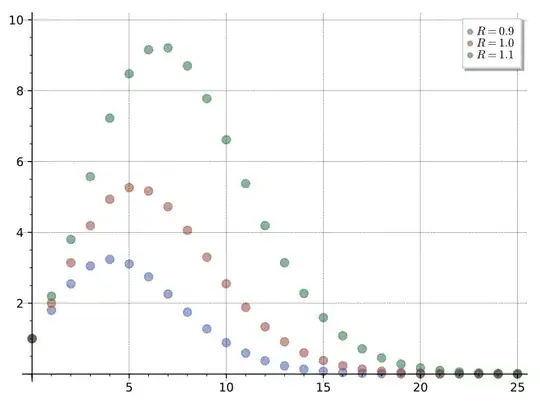
I mean, indeed that we can calculate the volume of n-dimensional vector embedding using that hyper volume formula.

$V_n(r)=\frac{\pi^{\frac{n}{2}}r^{n}}{\Gamma(1+\frac{n}{2})}$

So, is there a metric $M$ (analog to cosine similarity, euclidean distance, etc) that using Gamma function?

Maybe it's the ratio between two vectors using hyper volume: $M(a,b)=\frac{V(||a||)}{V(||b||)}$

So, what is the relationship between curse of dimensionality, volume in n-dimensional ball, and what it to do with n-dimensional vector embedding?

Answer 1

In high-dimension most of the volume of the unit ball is concentrated in a thin shell near the boundary due to many corners, and differences in distances or volumes can become very unintuitive. Therefore data becomes sparse in the ambient space and many usual metrics such as the Euclidean distances between points tend to concentrate, that is, the ratio of the distance between the nearest and farthest neighbor shrinks, cursing most metric-based ML models like KNNs, K-Means/GMM clustering, SVMs, density estimation KDE, etc.

When data actually lies on a lower-dimensional manifold, then metrics that don’t take this into account may be misleading. Similarly any metric that directly incorporates the Gamma function or your proposed volume ratio, which is essentially proportional to $(\frac{||a||}{||b||})^n$, are extremely unstable and unreliable for comparing embeddings when $n$ is very large.

In practice since cosine similarity is invariant to magnitude scaling, it often performs more robustly when magnitudes are less informative, which explains cosine similarity's wide usage in NLP tasks such as semantic search, clustering, and dense passage retrieval when working with embeddings from masked language models like BERT. Other non-masked/non-denoising/non-generative modeling approaches need to adapt the distance magnitude to better reflect the intrinsic structure of the data via multiview/multimodal feature learning like Siamese network with contrastive, triplet, InfoNCE, or Barlow Twins loss functions. Since the adaptively learned metric implicitly reflects a lower-dimensional manifold possibly free of the curse of dimensionality, multiview feature learning is also one of the most performant methods.