Why isn't class_weight='balanced' impacting my F1 score for an imbalanced dataset (SVM)

Question

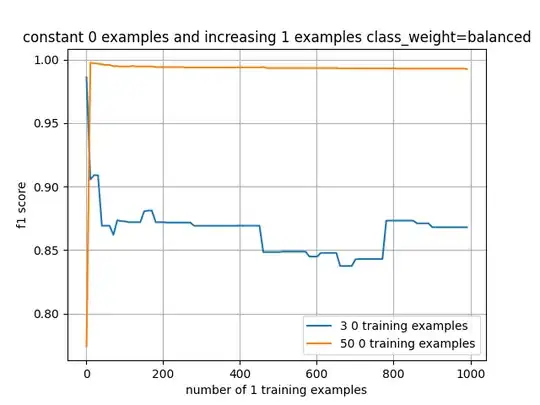
I'm using MNIST to test how a class imbalance can impact an SVM model.
I have a training set with 50 examples of '0'. I then am increasing the number of '1' training examples (starting from 1 example of '1' up to 999 examples of '1' in the training set) and retraining on each iteration.

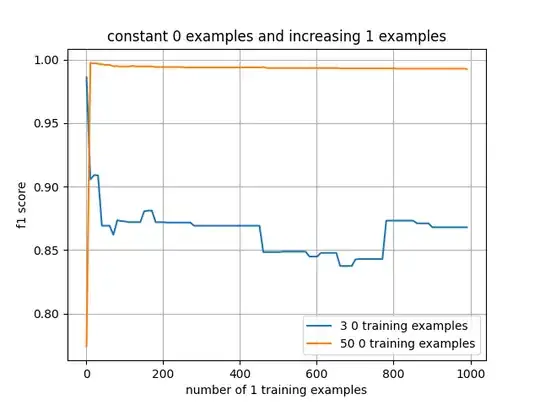
As you'd expect, the model trained with 50 '0' examples and 50 '1' examples does the best (and for 3 training examples, 3 '0' examples and 3ish '1' examples does the best).

In order to account for the class imbalance, I update the class_weights to be balanced by updating the code from:
clf = svm.SVC(kernel='linear')
to
clf = svm.SVC(kernel='linear', class_weight='balanced')
but the f1 score isn't impacted.

Why is this? You'd think that changing the class weighting would at least have some impact of the model selected.

Here is a snippet of the code:

for i in few_shot_examples:
        # 50 training examples
        # Creates a test-train split with 50 label1 examples and i label2 examples
        X_train, y_train, X_test, y_test = test_train_split_2_fewshot_labels(mnist, label1, 50, label2, i)
        # Train
        clf = svm.SVC(kernel='linear')
        clf.fit(X_train, y_train)
        # F1 Score
        y_pred = clf.predict(X_test)
        f1_scores_50.append(metrics.f1_score(y_test, y_pred, pos_label=label1))

or you can check out the entire test here:
https://github.com/Tyler-Hilbert/FewShot_SVM_Question/blob/b23a6e6cf6cc766e6c57295618a9e78d73ac121a/AllDigitCombinations/test_all_combinations.py

Answer 1

SVMs especially with a linear kernel are relatively robust to class imbalance because they rely on support vectors to determine the margin. If the support vectors are roughly representative of both classes, even when one class has many more examples, the decision boundary may not shift much when you adjust the weights.

When you set class_weight='balanced', scikit-learn svm automatically assigns weights inversely proportional to the class frequencies. However, the raw pixel-flattened intensity features for the two classes ("0" & "1" in your case) are well separated as often the case with MNIST digits which are relatively easy to distinguish, the reweighting might only cause a small adjustment in the decision boundary, insufficient to create a marked change in the overall F1 score as the harmonic mean of precision and recall.