Policy performance when the stationary state distribution is not unique in RL

Question

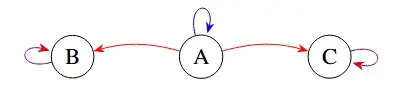
Consider the chainworld above with two actions, move (in red) and stay (in blue). Moving in A is stochastic: the agent moves to B with probability $p$ and to C with probability $1-p$. Moving or staying in B and C is irrelevant.
Clearly, there exists an optimal policy depending on the reward in A, B, C, the probability $p$, and the discount factor $\gamma$.

However, can the policy performance be defined? Consider the policy that does "move" in A: the induced Markov chain has two stationary state distributions $\mu_\pi$ (agent stays forever in B or C). Is the policy performance of this policy $J^\pi = \sum_s \mu_\pi(s) V^\pi(s)$ defined? We know that is it defined when the MDP is ergodic and $\mu_\pi(s)$ exists and is unique, but what about this scenario? The problem I see is that there are two $\mu_\pi(s)$ but $J^\pi$ does not account for that. Intuitively, I would simply weigh the sum by the probability that the agent induces the stationary distributions, i.e., $J^\pi = \sum_{\mu_\pi} p(\mu_\pi) \sum_s \mu_\pi(s) V^\pi(s)$. In the example above, $p(\mu_\pi)$ would just be $p$, but in more complex MPDs it may depend on multiple probabilities.

I haven't found anything like that in RL literature, and I was wondering why.

Answer 1

Indeed your idealized problem is an edge case which is less studied. Most practical problem-solving RL literature assumes that induced MCs from MDPs are ergodic which simplifies both theory and practice.

In many practical MDPs, even if there're non-ergodicity due to non existence of a single communicating class as you've perhaps known, the stationary distributions for policies don't split in such a clear-cut manner as you also imagined.

In RL policy performance is usually evaluated across many sampled induced trajectories which inherently handles your concerned stochasticity in transitions without explicitly decomposing into multiple stationary distributions.

Finally your approach requires explicit knowledge of environment's transition dynamics which is not directly accessible in most popular model-free RL methods such as all policy gradient based methods.

Having said that, Baumann et al (2023) "Non-ergodicity in reinforcement learning: robustness via ergodicity transformations" studies non-ergodic RL in terms of reliability via ergodic transformation which might suggest it's actually an important problem for some real world applications in terms of learned optimal policy's reliability when non-ergodicity does occur.

A significant challenge hindering the adoption of RL methods in these domains is the non-robustness of conventional algorithms. In this paper, we argue that a fundamental issue contributing to this lack of robustness lies in the focus on the expected value of the return as the sole ``correct'' optimization objective. The expected value is the average over the statistical ensemble of infinitely many trajectories. For non-ergodic returns, this average differs from the average over a single but infinitely long trajectory. Consequently, optimizing the expected value can lead to policies that yield exceptionally high returns with probability zero but almost surely result in catastrophic outcomes.