Can the limiting distribution depend on the initial distribution?

Question

I am a bit confused about the definition of limiting distribution in Markov chains.

My understanding is that it represents the behavior of the chain in-the-limit. That is, I start from the initial distribution $\mu_0(s)$ and repeat $\mu_1(s) = \mu_0(s) P$, $\mu_2(s) = \mu_1(s)P, \ldots$ and at some point the distribution will not change anymore. This seems also what this question/answer says.

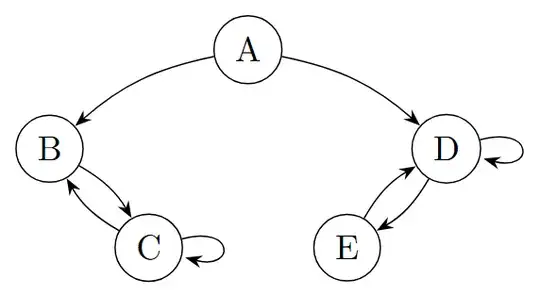
However, all definitions I find say that the limiting distribution does not depend on the initial distribution. But I can easily make a non-irreducible chain with two communicating classes like the one below, where the limit will converge but depends on the initial distribution.

So, can the limiting distribution depend on the initial distribution? If not, how can I find it?

This answer shows a few methods and one is what I am already doing below, i.e., a simple loop to simulate the chain. But, if I run it I converge to different distributions depending on the initial one.

import numpy as np
np.set_printoptions(precision=3, suppress=True)
P = np.array([
    [0.0, 0.5, 0.0, 0.5, 0.0],
    [0.0, 0.0, 1.0, 0.0, 0.0],
    [0.0, 0.5, 0.5, 0.0, 0.0],
    [0.0, 0.0, 0.0, 0.5, 0.5],
    [0.0, 0.0, 0.0, 1.0, 0.0],
])
MU = [
    np.array([0.3, 0.1, 0.2, 0.4, 0.0]),
    np.array([1.0, 0., 0., 0., 0.0]),
    np.random.rand(5),
]
for mu_t in MU:
    mu_t /= mu_t.sum()
    for _ in range(1000):
        mu_t = np.dot(mu_t, P)
    print(mu_t)
    print(np.dot(mu_t, P))
    print()

I know that an ergodic chain has only one unique limiting distribution and that my example is not ergodic, so I am considering the general case.

score 3 · Answer 1 · answered Nov 24 '24 at 23:19

Indeed the limiting behavior of a non-ergodic Markov chain which is not irreducible with multiple mean positive recurrent communicating classes depends on its initial distribution, since apparently the state space can be decomposed into multiple communicating classes thus the limiting distribution if exists depends on which class is activated by the initial distribution and typically there's one limiting distribution per recurrent communicating class if all states within the said communicating class are aperiodic.

In summary without irreducibility the limiting distribution if exists is not unique, and without aperiodicity a mere stationary distribution may not be converged as a limiting distribution as illustrated in the answer to your recent post here. There's conceptual difference between a limiting and stationary distribution of a MC.

Neil Slater · Accepted Answer · 2024-11-24T19:18:42.643

all definitions I find say that the limiting distribution does not depend on the initial distribution

The proof of this trait of the limit relies on the asumption of ergodicity.

You can define an MDP where there are non-interacting splits in trajectory (i.e. a branch in trajectory with no way of reaching outside of a subset of states), with two or more recurrent loops, plus an initial distribution where it is possible to reach at least two split points. This is essentially multiple ergodic MDPs in a branching structure. In that case, within each split, the limiting distribution is independent of the starting distribution.

In your example case, everything ends up in B & C or D & E. The ratio of times spent between BC and DE depend on the starting distribution. Within those groups, the ratios of time B:C and D:E are fixed and converge independently of any starting distribution.

Can the limiting distribution depend on the initial distribution?

2 Answers2