1

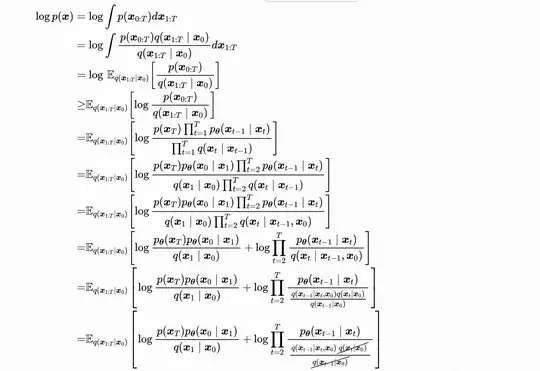
I was looking at the derivation of the ELBO for diffusion models from this website and I'm a little bit confused as to why they cancelled these two terms out.

enter image description here

nbro
  • 42,615
  • 12
  • 119
  • 217
henrysilver
  • 13
  • 2

1 Answers1

0

Indeed this sounds very confusing until you expand the product $\Pi$ terms as outlined below: $$\frac{p_{\theta}(x_1|x_2)q(x_1|x_0)p_{\theta}(x_2|x_3)q(x_2|x_0)...p_{\theta}(x_{T-1}|x_T)q(x_{T-1}|x_0)}{q(x_1|x_2,x_0)q(x_2|x_0)...q(x_{T-2}|x_{T-1},x_0)q(x_{T-1}|x_0)q(x_{T-1}|x_T,x_0)q(x_T|x_0)}$$

Therefore now it's obvious that the cancelation is from all alternating $q$ terms with only one conditioned variable $x_0$ in the numerator and denominator, respectively, except the first and last terms $\frac{q(x_1|x_0)}{q(x_T|x_0)}$ still remain. That's why in your reference the next step in show me proof section there appears one additional middle term $+\log \frac{q(x_1|x_0)}{q(x_T|x_0)}$. The author perhaps should expand like here to help reader's clear comprehension considering he's already written so many detailed steps.

cinch
  • 11,000
  • 3
  • 8
  • 17