I've tried to come up with a simple connection between statistics and deep learning. One question is:
- In very simplified terms, why do neural networks model probability distributions?
What I expect is an authoritative answer as to how this chain of thinking answers or not the above question, and whether it's directionally correct or not.
This is a minor answer to check with others whether this is directionally correct.
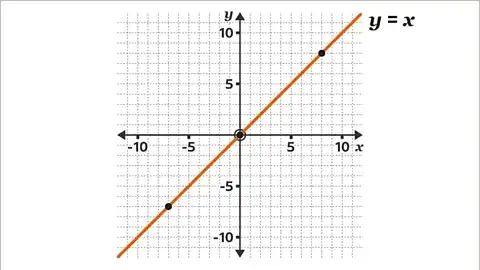
Had we just a line like so:
Then that's fully determined and there isn't any uncertainty on x or y.
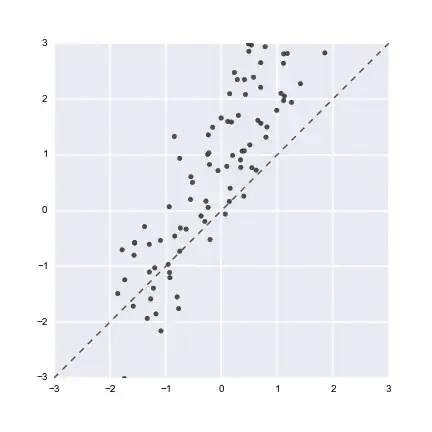
However, in this next case it's different:
The x values are distributed with some probability along x, and the correspondent is valid for y.
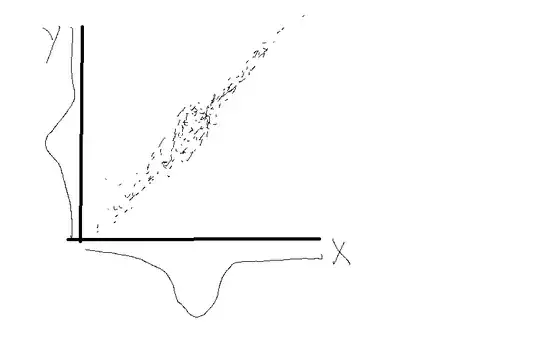
In some cases the probability on each axis may approach a Gaussian distribution, which I would draw as:
Obviously this does not need be the case, it's just an example.
If I understand correctly, both x and y can be considered random variables X and Y, and in that case, it's easy to see why neural networks learn probability distributions, what they actually learn is the function approximating the mapping (that reduces the error.)
In other words, neural networks model probability distributions.
So it should be clear there why one talks about statistics in deep learning, it's mostly about the spread in X, and Y. f: X ~=> Y Where f(X) is the complicated function / neural network. (In the learning process that's actually the Loss.)
As described in a similar way in Wikipedia for the Loss function:
Is this very simplified understanding correct at least directionally ?