Can a neural network learn dependencies that can be expressed only by iterative approaches?

Question

There are many relationships that cannot be described by a "static function" in N dimensions because relationships of the type I am talking about have an iterative element when one of the inputs of a function is its previous output.

Here is a specific toy example of an observation series where
I use this well-known formula for calculating the investment sum at the end of several periods:

 f(x) = s*(1+i)^x
s = starting sum
i = interest
X (variable) = number of periods.

BUT In this specific sub-case I calculate the final sum at the end of several periods with the addition of some fixed sum of money at the end of each period, in such case, the formula above doesn't work "as is" it has to become iterative taking as an input own output from the previous iteration. see image attached:

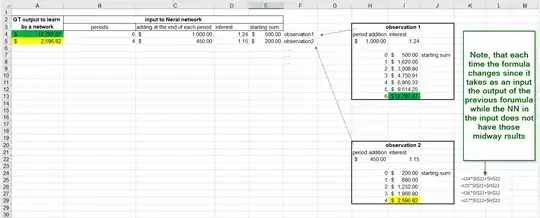
Thus I wonder whether in such case a NN can find a dependency and predict similar cases as those in the two proposed observations of a training set. If yes, it is quite strange because after all a NN fits a curve to the input data points and this curve is actually a static function, but as seen from the Excel image in this case there is no "static function", since the function there is kinda recursive.

Answer 1

Your example may still be framed as a static function, if in addition to s, i and x, you also provide y = fixed sum increment per year:

$$f(x) = s(1+i)^x + \sum_{n=1}^{x-1} y(1+i)^n$$

(This assumes you do not include a final payment at end of year x). Note this function does not simulate the process in the same way as your spreadsheet example, but does calculate the correct output.

Despite the fact in this case I could find a function that wasn't a direct simulation of the example process, there do exist plenty of situations where this is not possible, and the most direct way to calculate a correct value is to follow a multi-step process. The compound interest function would become like that if there was anything non-linear applied between each step - some banks offer a variable interest rate depending on how much is in the account for instance, and if that applied here, it would prevent the decomposition I used in the above function.

With machine learning, it is reasonably common to use parametric static functions to predict/approximate the outcome of some more complex process. This is different to modelling the process, and does have limitations when the process can behave chaotically or randomly. However, just because an underlying process is complex does not prevent there being usable correlation between starting inputs and outputs.

Statistical learners such as neural networks don't care how complex the internal logic is for your problem, or even which way causality might flow. If there is a correlation between inputs and outputs, and enough data to learn from, then a machine learning model may be trained and perhaps able to make useful predictions. This is not guaranteed, but it is also not prevented purely due to inputs and outputs being related via a multi-step process. It is also not the same as learning to model the process - unless very carefully constructed and trained, neural networks don't ever learn how something is calculated, instead they learn the "shape" of an output function within the bounds of the training data.