How the Q,K,V be calculated in multi-head attention

Question

I want to understand the transformer architecture, so I start with self attention and I understand their mechanism, but when I pass to the multi-head attention I find some difficulties like how calculate Q , K and V for each head. I find many way to calculate Q , K and V but I don't know which way is correct.
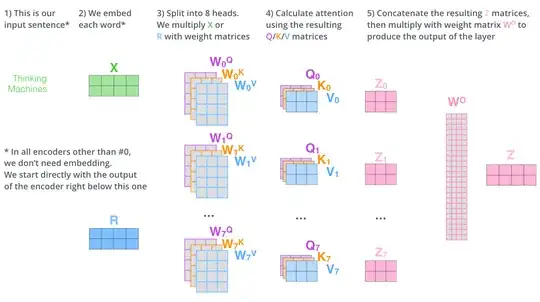
method 1: method 2: I find this method in YouTube. method 3: in this method it just for headi we have: Qi=xWqi Ki=xWki Vi=xWvi so I don't know which method is correct there is the links of my references The Illustrated Transformer YouTube video

Answer 1

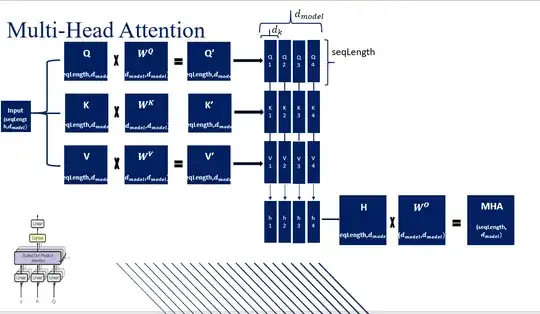
As far as I understand your question, you have problems with multiple heads. Let's take the input $\mathbf{Q}$ (with dimension: $\textit{seq_length}$ x $d_{model}$), which is the same for $\mathbf{Q}, \mathbf{K}$ and $\mathbf{V}$ (thus $\mathbf{Q} = \mathbf{K} = \mathbf{V}$). then you need to multiply them with 3 different matrices (with dimension: $d_{model}$ x $d_{model}$), thus: $\mathbf{Q}$ x $\mathbf{W}_{q}$, $\mathbf{K}$ x $\mathbf{W}_{k}$, $\mathbf{V}$ x $\mathbf{W}_{v}$. Why this multiplication? Because those are the matrices with the learnable parameters. Now... in case of multi head attention, you need to split them by the number heads, that you want. Since the model dimension ($d_{model}$) must be divisible by the number of heads ($h$). At this point you do not need to create or use any complicate function, you can just reshape the three matrices in this way:

# (batch, seq_len, d_model) --> (batch, seq_len, h, d_k) --> (batch, h, seq_len, d_k)

or in PyTorch code if you prefer:

query = query.view(query.shape[0], query.shape[1], self.h, self.d_k).transpose(1, 2) (where d_k = dim_model // h)

In case you don't "see" the division in chunks, open a terminal, import torch and try the line of code above (removing the batch in all the calculation) allright?

Answer 2

Given the input $x$ into the head, Q, K, and V are simply $x$, but then adapted by distinct fully connected neural network layer.

To clarify, each head has 3 linear layers, one for constructing Q, one for constructing K, and one for constructing V. The input for each of these linear layers is just a copy of $x$. Each head (of multi head attention) has their own set of parameters.

Notably, these learnable linear layers are the only learnable parameters of the head.